¿Cuál sería la solución a esta integral?
Aplicando las propiedades y definición de integral, ¿Cuál sería la solución a esta integral?
Gracias.
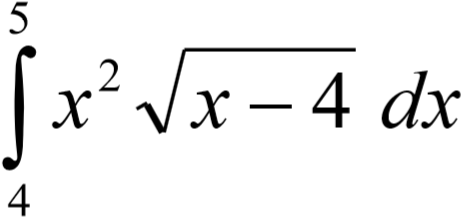
1 Respuesta
Respuesta de Lucas m
2
