;)
Hola Monse!
Te hago primero la primera integral.
Para ello hemos de dibujar el recinto y buscar los puntos de intersección.
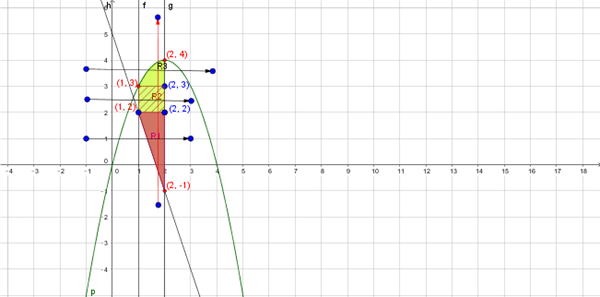
La primera integral dy dx se hace para un recinto tipo 1. Por el método de las flechitas observa la flecha vertical de color rojo: entra por un punto y sale por otro, luego es tipo 1
La integral : las x son el intervalo [1,,2]
y las y van de la recta y=-3x+5 y salen por la parábola y=4x-x^2,
luego la primera integral es:
$$\begin{align}&\int_{x=1}^{x=2} \int_{y=-3x+5}^{y=4x-x^2}f(x,y) dy dx\end{align}$$luego es correcta.Nos piden cambiar los limites de integración a dx dy, para ello comprobamos que tambien es un Recinto tipo II. Por el método de las flechitas, observa las flechas horizontales, entran por un punto y salen por otro punto. Luego si es Tipo II. Hay que descomponer la integral en tres integrales dobles:
Recinto 1: entra por la recta x=(5-y)/3 y sale por la recta x=2.
Las y van de [-1,2]
Recinto 2: Entran por x=1 y sale por x=2
las y van [2,3]
Recinto 3: Entra por la parábola(habrá que despejar la x) y sale por x=2
Las y van de [3,4]
Despejamos la x en laparábola:
$$\begin{align}&y=4x-x^2\\&x^2-4x+y=0\\&\\&x= \frac{ 4 \ \pm \sqrt {16-y^2}}2\\&\end{align}$$hay dos x, una para la rama de la izquierda de la parábola y otra para la rama de la derecha. Entra por la de la izquierda que es fácil comprobar que es
$$\begin{align}&x= \frac{ 4 - \sqrt {16-y^2}}2\end{align}$$Luego las tres integrales que hay que plantear son:
$$\begin{align}&R1= \int_{y=-1}^{y=2} \int_{x= \frac{5-y}3}^{x=2} f(x,y)dxdy\\&\\&\\&R_2=\int_{y=2}^{y=3}\int_{x=1}^{x=2} f(x,y) dx dy\\&\\&R_3=\int_{y=3}^{y=4} \int _{x= \frac{ 4 - \sqrt {16-y^2}}2}^{x=2} f(x,y)dxdy\end{align}$$Saludos
;)
;)


