Que diferencia hay en los criterios de la primera deriva y los de la segunda derivada?

;)
El criterio de la primera derivada para extremos relativos:

1º Calcular los puntos donde la recta tangente es horizontal y'=0 ( gráficamente puede ser un máximo relativo, o un mínimo relativo, o un Punto de inflexión con tangente horizontal)

Hay puntos de inflexión donde la tangente no es horizontal

2º Para saber cual de los tres casos es, estudiar el signo de la primera derivada (crecimiento)

A la izquierda y a la derecha de los puntos críticos(y'=0).

Si cambia el signo de positivo a negativo ==> máximo relativo

Si cambia el signo de negativo a  positivo ==> mínimo relativo

Si no cambia el signo ==> punto de inflexión con tangente horizontal. En los puntos de inflexión cambia la concavidad pero no el crecimiento

Ejemplo

$$\begin{align}&y=x^3-3x^2\\&\\&y'=3x^2-6x\\&\\&y'=0==>3x(x-2)=0\\&x_1=0\\&x_2=2\\&\\&Ordenadados \ de \ menor \ a \ mayor:Intervalos\\&(-\infty,0)==> f'(-10)=300+60>0==>creciente\\&\\&(0,2) ==> f'(1)=3-6<0 ==> decreciente\\&==>el\ punto \ (0,f(0))=(0,0)\ es \ máximo \ relativo\\&\\&(2, \infty)==> f'(10)=300-60>0 ==> \ creciente\\&===> el\ punto \ (2,f(2))=(2,-4)\ es \ mínimo \ relativo\end{align}$$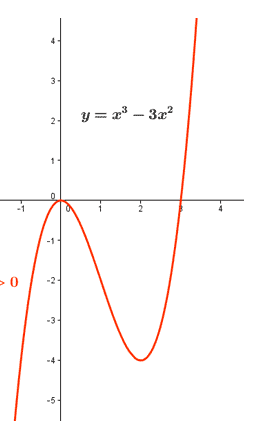

El criterio de la segunda derivada para máximos y mínimos relativos, se basa en estudiar el signo de la derivada segunda en los mismos puntos críticos, x=0 y x=2, no a izquierda ni a derecha.

Observa que en el máximo es convexa o hacia abajo, y en el mínimo es cóncava (o hacia arriba)

Ojo que creo que los americanos lo consideran al revés, por eso prefiero hablar de hacia abajo (o hacia arriba) en lugar de convexo (o cóncavo)

La concavidad-convexidad se estudia con el signo de la segunda derivada:

y''>0  ==> hacia abajo 

$$\begin{align}&\cap\end{align}$$

y''<0==> hacia arriba

$$\begin{align}&\cup\\&\end{align}$$

Observa que el criterio de la derivada segunda, el primer paso es el mismo: puntos críticos y'=0

Salen x=0  y  x=2

$$\begin{align}&y''=6x-6\\&\\&y''(0)=-6<0 ==>máximo(hacia arriba)\\&y''(2)=12-6>0 ==>mínimo (hacia \ abajo)\end{align}$$

Los puntos donde la función no es cóncava ni convexa se llaman puntos de inflexión , y enestos puntos la derivada segunda  ni es positiva ni es negativa, luego y''=0

6x-6=0

x=1 ==> P.I.  (1,f(1))=(1,-2)

Observa que si calculas la pendiente en este punto de inflexión: y'(1)=3-6=-3 <0 es decreciente

Este punto de inflexión no tiene la tangente horizontal por eso no es un punto crítico.

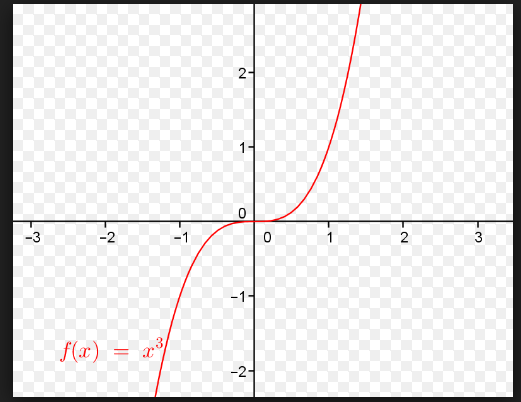
Ejemplo 2

$$\begin{align}&y=x^3\\&\\&y'=3x^2=0==> x=0\\&\\&(-\infty,0)==>f'(-10)=300>0==>creciente\\&(0,\infty)==> f(10)=300>0 ==> creciente\\&\end{align}$$

como es un punto crítico (y'=0) pero el crecimiento no cambia ==> es un punto de inflexión de tangente horizontal.

Todos los puntos de inflexión cumplen y''=0

y''=6x=0 ==> x=0

La concavidad a la izquierdas de concavidad

(-infty,0) y''(-10)=-60<0  hacia abajo (^)

(0,+infty) y''(10)=60>0 hacia arriba (U)

Luego es un punto de inflexión claramente (0,0)

Para estudiar el crecimiento con el primer criterio tienes suficiente. Cuando son funciones polinómicas suelo usar el segundo criterio, ya que la derivada segunda es rápida.

Saludos

;)

;)

Muchísimas gracias Lucas, me ha servido muchísimo :)

utilizas Intervalo abierto, (a, b),  (menores que a y menores que b.)

por que?