Como hago este ejercicio de derivadas por definición

Quiere que use esta formula
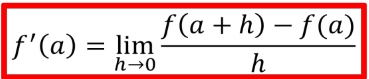
¿Cómo lo resuelvo?
1 Respuesta
Respuesta
1

Quiere que use esta formula
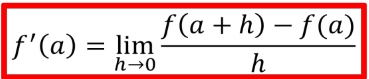
¿Cómo lo resuelvo?
