Anónimo
1. Solución y aplicación de problema de conservación
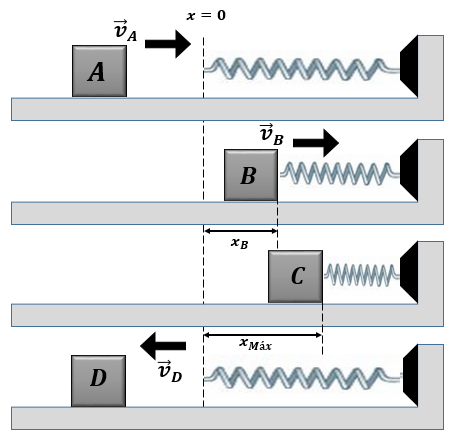
El resorte de la figura 1 está apoyado sobre la superficie horizontal y tiene su extremo derecho asegurado a la pared. Su constante elástica vale k1 125 N/m. El bloque tiene masa m1 0,762 kg y es lanzado en el punto A hacia el resorte, apoyado en la superficie, con rapidez vA 3,10 m/s. Todas las superficies en contacto carecen de rozamiento.
- Determine la rapidez del bloque cuando está pasando por la posición B, donde la compresión del resorte vale xB 0,135 m.
- Determine la máxima compresión que el bloque produce en el resorte (esta posición está marcada C en la figura; ¿x_"max" =?)
- Determine la rapidez del bloque después de que ha vuelto a perder contacto con el resorte (posición D en la figura).
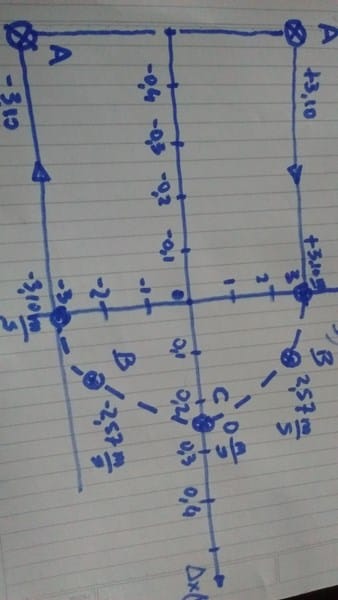
La figura usa un eje “x” horizontal, positivo hacia la derecha, que corre a lo largo del eje del resorte. El origen x=0 está ubicado en el punto del extremo izquierdo del resorte no deformado, como lo muestra la primera subfigura. Para la coordenada “” del bloque, use su cara frontal (la del lado del resorte). El contacto entre bloque y resorte comienza entonces en la coordenada . Si la coordenada “” del bloque en las posiciones A y D es xA, D -0,474m, trace una gráfica cuantitativa (ejes marcados numéricamente) de la rapidez del bloque contra su posición ( en el eje Y, x en el eje X). La gráfica debe cubrir todo el movimiento del bloque desde A hasta D,
1 Respuesta
a) Energia cinetica del bloque original = 1/2 m v^2 = 0.5 x 0.762 x 3.10 ^2 =3.66 Joules.
Luego de tocar el resorte, el bloque estara sometido a dos acciones:
E.C. bloque en posicion B = E.C. original - Energia potencial del resorte comprimido 0.135 m
3.66 - 1/2 k ( delta l)^2 = 3.66 - 0.5 x 125 x 0.135^2 = 2.52 Joules
2.52 = 0.5 x 0.762 x V(B)^2 ......................V(B) = 2.57 m/s
b) Para la posicion de maxima compresion corresponderia a que toda la energia cinetica del bloque se transformo en E.P. elastica del resorte comprimido...
3.66 = 0.5 K ( DELTA X)^2 ..........................Xmax. = (3.66 / 0.5 x 125 )^1/2=0.242 m
c)Al perder contacto con el resorte siendo- campo de fuerzas conservativo- el bloque sera lanzado con la velocidad que traia al impactar pero en sentido contrario... V( posicion D) = - 3.10 m/s.
El grafico que te piden no es tema dificil. Lo podes encarar vos. Si necesitas te hago el esquema.
Me gustaría que me colaborara con el esquema para la respectiva visualización. Muchísimas gracias.
Si, pero disculpa la desprolijidad.
Es lo que yo interpreto del enunciado que te dan.Eje +x hacia la derecha..........eje +v hacia arriba.