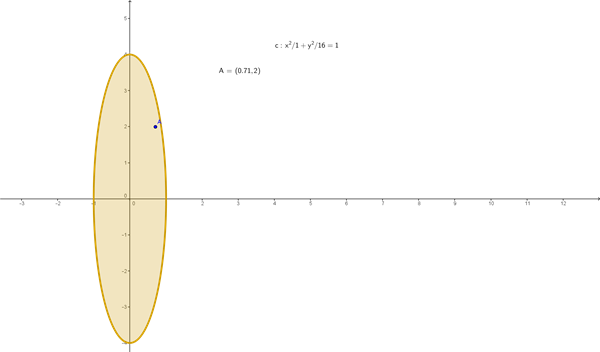
Ecuación de la elipse con datos de vértice y punto por el cual pasa
Como puedo plantear la ecuación de la elipse si con vértice en (0,4) y pasa por el punto
$$\begin{align}&({\sqrt2\over2},2)\end{align}$$las opciones que tengo son las siguientes
$$\begin{align}&A) \ \ \ \ x^2+{y^2\over16}=1\\&B) \ \ \ \ {x^2\over16}+y^2=1\\&C) \ \ \ \ {x^2\over4}+y^2=1\\&\\&D) \ \ \ \ x^2+{y^2\over4}=1\end{align}$$
1 respuesta
Respuesta de Lucas m
2