La grafica de la funcion f(x) es la siguiente
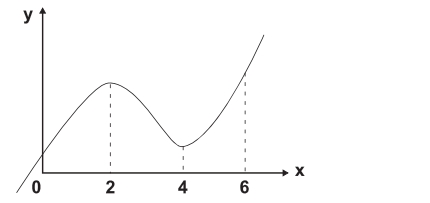
¿En qué intervalo la derivada de f es negativa?
3 respuestas
La derivada será negativa cuando la función esté 'bajando'. Por lo que se puede ver en esta imagen eso ocurre para x en el intervalo (2, 4)
Salu2
Para hallar la pendiente se utiliza
$$\begin{align}& \frac{y-y_{0}}{x-x_{0}} = m\\&Si\\& y < y_{0} → m \ es \ negativa\end{align}$$Entonces, en el problema es el intervalo (2 , 4)
;)
Hola Gabriel!
La derivada de la función es la pendiente de la recta tangente.
La derivada negativa implica pendientes negativas, lo cual implica función decreciente.
Recuerda que las funciones se miran de izquierda a derecha.
Luego observamos que es decreciente en el intervalo de x (2,4)
Saludos
;)
;)
;)
Lucas, ¿por qué el intervalo es abierto? ¿Por la fórmula de pendiente en donde para el denominador condicionamos que no puede ser cero el denominador?
;)
Porque justo en los extremos del intervalo: x=2 i x=4, las rectas tangentes son horizontales:
en x=2 máximo relativo
en x= 4 mínimo relativo
En esos puntos, que son los que definen los intervalos de crecimiento, la función i crece ni decrece(y'=0)
;)
;)
oh muy bien, puede llegar a presentarse un caso con intervalo cerrado? supongo que seria cuando no hay ni máximo ni mínimo, sino que se mantiene
Lucas, esta viendo la respuesta a este ejercicio y veo que es
(2,4]
por que?
;)
Yo diría que no es correcto.
Cuando escribes los intervalos de crecimiento, siempre son intervalos abiertos, porque los puntos que delimitan esos intervalos son los de y'=0 (con lo cual ni crece ni decrece), o bien las asíntotas verticales que no existe función:
http://www.vitutor.com/fun/5/c_8.html
;)
;)
checa este video Lucas
https://www.youtube.com/watch?v=KzzwdwUba1M
en el minuto 54 manejan este caso,
;)
Para mi eso es incorrecto totalmente.
El mismo dice que tiene pendiente negativa después de 2, antes de 2 es positiva.Luego en 2 es 0 y la función allí ni crece ni decrece. El razonamiento es el mismo para x=4.
No entiendo la diferencia.
Yo los pondría abiertos.
Lee el punto 3 del ejemplo de intervalos de crecimiento:
http://www.universoformulas.com/matematicas/analisis/crecimiento-decrecimiento-funcion/
No conocía !checa!! (=mirar!!
;)
;)