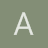Hallar el área de la región limitada por la función f(x)=senx, entre x=0 y x=2π. El área se expresa en unidades de superficie
Hallar el área de la región limitada por la función f(x)=senx, entre x=0 y x=2\pi . El área se expresa en unidades de superficie. Hallar el área de la región limitada por la función f(x)=senx, entre x=0 y x=2\pi . El área se expresa en unidades de superficie.
Hallar el área de la región limitada por la función f(x)=senx, entre x=0 y x=2\pi . El área se expresa en unidades de superficie.
Hallar el área de la región limitada por la función f(x)=senx, entre x=0 y x=2\pi . El área se expresa en unidades de superficie.
2 respuestas
Es igual a cero para f(x)= sin(x)
El area bajo la curva de la función la obtienes sacando la integral de la función f(x) evaluada en los valores que te dan.
En este caso es la integral de sen(x) evaluada entre 0 y pi/2
Recuerda que una integral de f(x) evaluada desde A a B, se resuelve como F(B) - F(A) .../ donde F es la función ya integrada y evaluada en los valores.
- cos(pi/2) - 0 = 0
Nooo, me equivoquée. No consideres esto