¿Cuál es la ecuación de la asíntota vertical de la función *
A) x = 3
B) y = - 3
C) x = - 3
D) y = 3
1 Respuesta
;)
Hola gabriel!
¿Cómo van los logaritmos?
¿Los tienes claros ya?
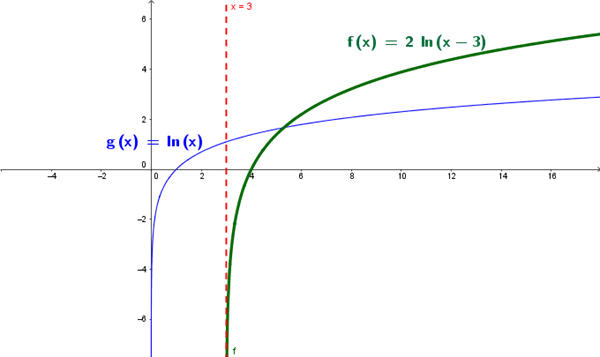
Para recordarte alguna propiedad has de tener en cuenta que solo existen logaritmos de números positivos, luego el Dominio de esa función se calcula resolviendo
El argumento mayor que 0
x-3 >0
x>3
Domf=(3, + infinito)
Se calcula igual que las irracionales
$$\begin{align}&y=\sqrt{x-3}\\&\\&x-3 \geq0\\&\\&x\geq3\\&\\&Domf=[3,+\infty)\end{align}$$con la única diferencia que en los radicales , el radicando si puede ser 0. Por eso
$$\begin{align}&y= \sqrt{u(x)}\\&==>\\&u(x)\geq0\\&\\&\\&y=ln(u(x))\\&==>\\&u(x) >0\end{align}$$Observa que el argumento (x-3) es un polinomio, es contínuo.
Las asíntotas verticales, en las logarítmicas , suelen estar en la frontera.
Para ellos has de memorizar un resultado:
$$\begin{align}&\lim_{x \to 0}ln(x)=-\infty\\&\\&\lim_{x\to 3}ln(x-3)=-\infty\end{align}$$Asíntota vertical: x=3
Saludos
;)
;)
Ya los voy dominando un poco más, aquí tenia la duda por ese dos que esta multiplicando pero por la propiedad es igual a
$$\begin{align}&Log(x-3)^2\end{align}$$Muchas Gracias Lucas!
