Cálculo Integral: Si la función de densidad de probabilidad...
Si la función de densidad de probabilidad para la variable aleatoria X está dada por la expresión:
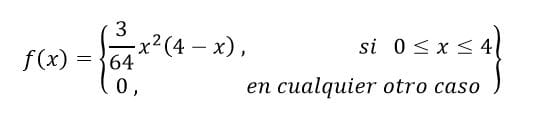
Determinar la probabilidad de que por lo menos la variable adquiera el valor 2.
1 respuesta
Lo plantearías como probabilidad de que X ( ALEATORIA) tome valores entre a y b seria la INTEGRAL definida de la función densidad de probabilidad dentro del intervalo.
El area que encierra la curva f(X) entre x=0 y x= 4 debe ser = 1 porque se trata de una distribucion de probabilidades.
Los valores que te toma la variable aleatoria serian todos los reales entre 0 y 4 . Luego lo que te piden es; (1 - probabilidad de que X tome valores comprendidos entre 0 y 2).
1 - INTEGRAL ( 3/64 x^2(4-x)) dx definida entre 0 y 2:
Si la resolves por partes llegarías a que la probabilidad de que x se halle entre 0 y 2 sería= 5/16
Luego la probabilidad que te estan pidiendo( complemento de la anterior) = 1 - 5/16 = 11/16 = 0.6875.
