Tengo duda con este ejercicio de calculo multivariado

;)
Hola Johana!

Tal como yo lo haría:

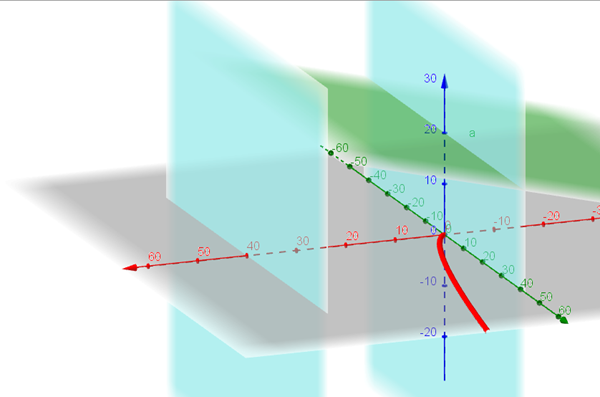
El eje X es el rojo, el Y el verde, el Z el azul.

La pared seria la definiría la curva  roja que sube desde z=0 a   z=20+ x/4 con    0<=x<=40

Proyectando la pared en el plano XZ, parametrizo la superficie como:

$$\begin{align}&F(x,z)=(x,x^\frac 3 2,z)\\&donde \\&\phi(x,z)=x^\frac 3 2\\&\\&\\&dS= \sqrt{1+ (\frac{\partial \phi}{\partial x})^2+(\frac{\partial \phi}{\partial z})^2}\ \ dx\ \ dz=\\&\\&\sqrt{1+(\frac 3 2 x^\frac 1 2)^2+0^2}dxdz=\sqrt {1+ \frac 9 4 x}\ \ dzdx\\&\\&A=\iint_{A(\phi)}dS=\int_{x=0}^{x=40} \Bigg[\int_{z=0}^{z=20 +\frac x 4} \sqrt {1+ \frac 9 4x}\ \ dz\Bigg] \ dx=\\&\\&\int_0^{40}  \sqrt {1+ \frac 9 4x}\ \Big[z \Big]_0^{20+ \frac 1 4 x}dx=\\&\\&\\&\int_0^{40}  \sqrt {1+ \frac 9 4x}·\Big(20+ \frac 1 4 x \Big)dx\end{align}$$

Esa integral se hace por partes:

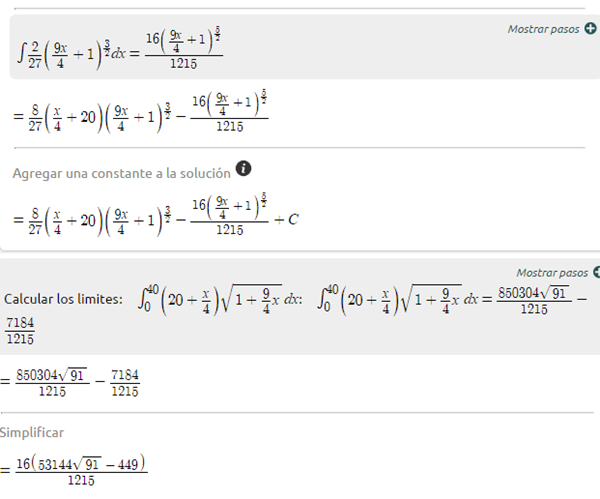
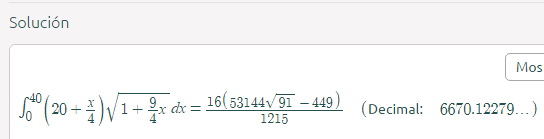
Saludos

;)

;)