Asíntotas de la siguiente función
Asíntota vertical, horizontal y oblicua de la función x^3/(x^2+1)
1 Respuesta
Respuesta
1
Las asíntotas verticales en una función fraccionaria suceden cuando el denominador vale 0, en este caso
x^2 + 1 = 0
x^2 = -1 no tiene solución, por lo tanto no tiene asíntotas verticales
Antes de ver si tiene asíntotas oblicuas, vamos a ver si tiene horizontales
$$\begin{align}&\lim_{x \to \pm \infty} \frac{x^3}{x^2+1}=\pm \infty\\&\text{No tiene asíntotas horizontales, veamos si tiene oblicuas}\\&\text{La recta asíntota sería de la forma y=mx + b}\\&m = \lim_{x \to \pm \infty} \frac{f(x)}{x}=\lim_{x \to \pm \infty} \frac{x^3}{x(x^2+1)}=1\\&b = \lim_{x \to \pm \infty} {f(x)} - m{x} = \lim_{x \to \pm \infty} \frac{x^3}{x^2+1}-x=\\&\lim_{x \to \pm \infty} \frac{x^3-x(x^2+1)}{x^2+1}=\lim_{x \to \pm \infty} \frac{x^3-x^3-x}{x^2+1}=\\&\lim_{x \to \pm \infty} \frac{-x}{x^2+1}=0\\&\text{Por lo tanto la asintota oblicua es }y=x\end{align}$$Te dejo la imagen de la función y su asíntota
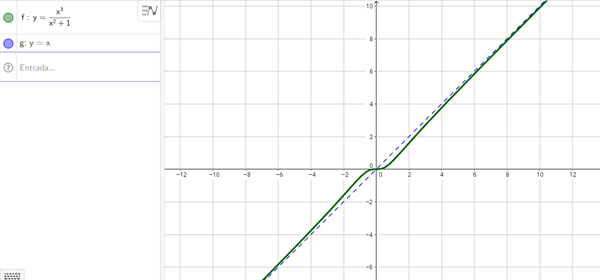
Salu2