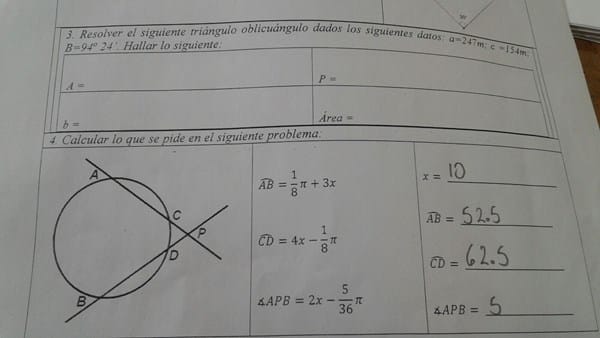
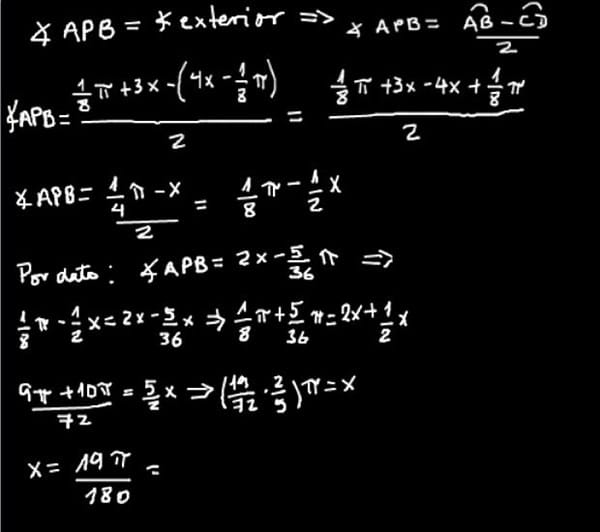Lo que piden es lo de la derecha que está respondido con lápiz ¿verdad?
A mí me da otro resultado.
En el libro de Geometría plana y del espacio y trigonometría de Aurelio Baldor, te vienen muy bien explicados, con demostraciones paso a paso de los teoremas para la resolución de este tipo de problemas.
Ok, Teorema de la medida del ángulo exterior: La medida del ángulo exterior es igual a la semidiferencia de las medidas de los arcos comprendidos por sus lados.
Operando te dará un resultado que hay que igualarlo con el dato que dan en el problema. Luego despejas x y tendrás el valor numérico, luego ya sólo es reemplazar y tendrás todos los otros valores.
Aquí como he hecho la primera parte, lo demás te lo dejo para que lo resuelvas con tu hija. Mucha suerte. Un saludo.
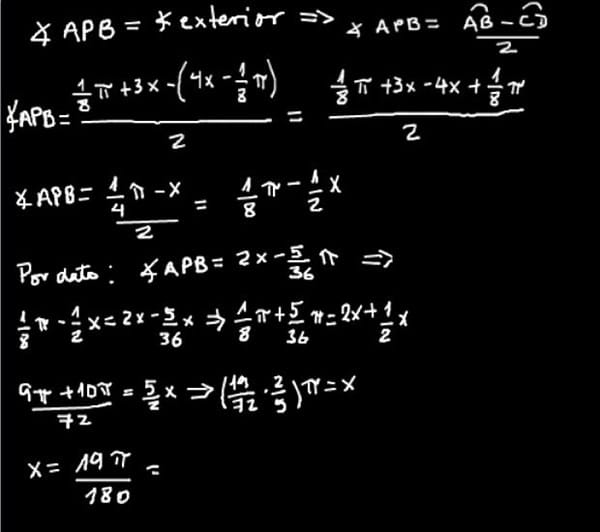
Sube las otras preguntas una a una, para poder visualizarlas mejor. Intentaré ayudarte.