Relación de transformación para pasar de coordenadas cilíndricas a esféricas
¿Cómo se halla la relación de transformación entre dos tipos de coordenadas?
¿Y para el caso concreto del paso de cilíndricas a esféricas?
2 respuestas
;)
Hola ana pola!
Las cilíndricas son:
$$\begin{align}&(r, \theta,z)\\&\\&Esféricas:\\&(\rho, \theta, \phi)\\&\\&observando\ el \ gráfico:\\&\rho=\sqrt{r^2+z^2}\\&\\&\theta=\theta\\&\\&\phi=arctan \frac r z\end{align}$$Saludos
;)
;)
Como se construiría la matriz jacobiana que las relaciona
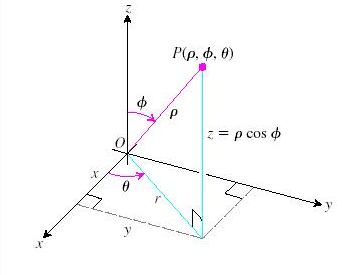
;) Tenemos la transformación
$$\begin{align}&f(r, \theta,z)=(\rho,\theta,z)=(\sqrt{r^2+z^2} , \ \theta,\ arctan \frac r z)\end{align}$$La primera fila del Jacobiano son las derivadas parciales de rho, respecto r, theta y z, respectivamente.
La segunda son las derivadas parciales de theta, respecto r, theta y z.
La tercera fila son las derivadas de phi, respecto de r, de theta y z, respectivamente.
Así en la primera columna tenemos todas las derivadas parciales respecto r.
En la segunda columna todas las derivadas parciales respecto theta
En la tercera columna todas las derivadas parciales respecto z.
$$\begin{align}&f_r=\frac {\partial f}{ \partial r} \\&\\&Jacobiano=\\&f1_r \ \ \ f1_{\theta} \ \ \ f1_z\\&\\&f2_r \ \ \ f2_{\theta} \ \ \ f2_z\\&\\&f3_r \ \ \ f3_{\theta} \ \ \ f3_z\\&\\&f1= \rho=\sqrt{r^2+z^2}\\&f2= \theta=\theta\\&f_3=\phi=arctan \frac r z\\&\\&f1_r=\frac{r}{\sqrt {r^2+z^2}} \ \ \ \ \ \ \ f1_{\theta}=0 \ \ \ \ \ \ \ f1_{z}=\frac z { \sqrt{r^2+z^2}}\\&\\&\\&f2_r=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ f2_{\theta}=1\ \ \ \ \ \ \ \ f2_z=0\\&\\&f3_r=\frac{\frac 1 z}{1+(\frac r z)^2}\ \ \ \ \ \ f3_{\theta}=0 \ \ \ \ \ \ \ \ f3_z=\frac{- \frac r {z^2}}{1+( \frac r z)^2} \end{align}$$Saludos y recuerda votar
;)
;)
$$\begin{align}&f(r, \theta,z)=(\rho, \theta, \phi)\end{align}$$error de escritura
;)
¡Muchas Gracias!
Entonces si queremos la matriz jacobiana que nos lleva de esféricas a cilíndricas sería al contrario las derivadas de las coordenadas esféricas respecto las cilíndricas?
Si, es el Jacobiano inverso.
Las matrices de los Jacobiano inversos, son inversas.
Con lo que los determinantes (jacobianos)son inversos.
Así si uno da r, el inverso da 1/r
;)
;)
Para referir un punto del espacio dado en coordenadas cilíndricas (ro, fi, z) a esféricas podes siempre:
1°)Pasar de cilíndricas a cartesianas según:
x= ro cos fi ........................y= ro sen fi .......................z= z
2°) pasar de cartesianas a esfericas ( r, fi, theta ) segun:
r= V(x^2 + y^2 + z^2)
fi = arc. cos (z/r)
theta = arc. tg. (y/x)