¿Cómo calcular la superficie en m2 de un circulo del que se desconoc el radio?
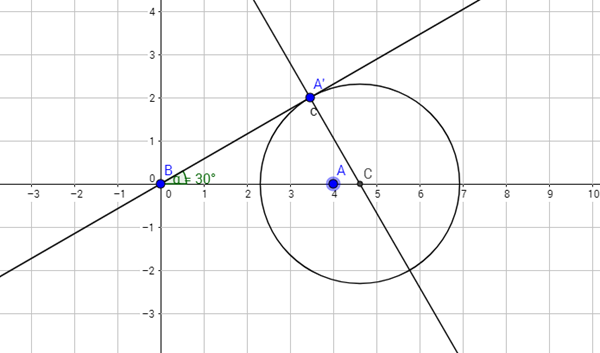
Necesito calcular los m2 de superficie de un circulo, y según creo la fórmula es πr2.
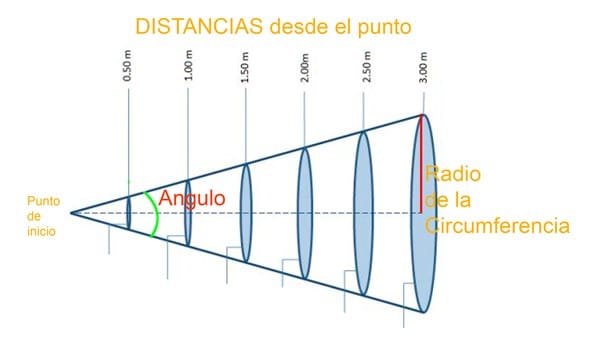
El problema es que desconozco el radio de dicho circulo, porque depende de la distancia a la que se encuentra dicho circulo de un punto. El tamaño de dicho circulo encaja dentro de un angulo que parte de dicho punto y que puede variar.
Existiría alguna fórmula que permita con estos parámetros hacer dicho calculo de los m2 de superficie, ¿pudiendo variar los mencionados angulo y distancia del punto?
1 respuesta
Respuesta
1