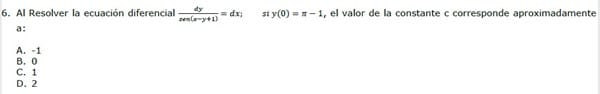Quien puede hallar aproximadamente el valor (ecuación diferencial)

Tienes el siguiente procedimiento,

$$\begin{align}&\dfrac{dy}{\sin(x-y+1)}=dx\longrightarrow\dfrac{dy}{dx}=\sin(x-y+1)\\&\textrm{reduccion a separacion de variables, y consideras},\\&u=x-y+1\\&\textrm{derivas}\\&\dfrac{du}{dx}=1-\dfrac{dy}{dx}\longrightarrow\dfrac{dy}{dx}=1-\dfrac{du}{dx}\\&\textrm{pero éste valor lo podemos reemplazar en la ecuación inicial, así,}\\&\left(1-\dfrac{du}{dx}\right)=\sin(u)\\&dx=\dfrac{du}{1-\sin(u)}\end{align}$$

y ésto ya es mucho más fácil de integrar, así que te recomiendo que la termines

$$\begin{align}&x=-\dfrac{2}{\tan\left(\dfrac{x}{2}\right)-1}+C\\&\textrm{sabemos que:  }y(0)=\pi-1\\&\\&x=-\dfrac{2}{\tan\left(\dfrac{x-y+1}{2}\right)-1}+C\\&0=-\dfrac{2}{\tan\left(\dfrac{0-(\pi-1)+1}{2}\right)-1}+C=-\dfrac{2}{\tan\left(\dfrac{-\pi+2}{2}\right)-1}+C\\&Supongamos: \tan\left(\dfrac{-\pi+2}{2}\right)-1=k \textrm{   es un número, entonces }\\&\\&0=-\dfrac{2}{k}+C\\&0=-2+kC\\&\textrm{pero: }kC=C_{1},entonces,\\&0=-2+C_{1}\\&\\&C_{1}=2\end{align}$$

y eso sería todo...ten en cuenta que hice ese cambio de ponerle el nombre "k", porque justamente no nos interesa el valor de ese horror, solo sé que es un número y ya...