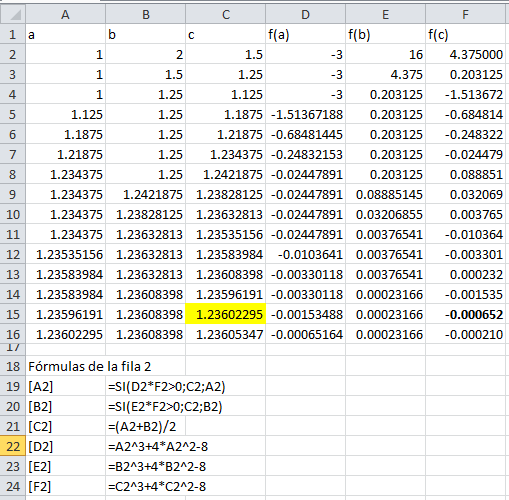
Demostrar que f(x) = x3 + 4x2 – 8 tiene una raíz en[1, 2] y utilizando el Método de bisección determineuna aproximación a
Serian tan amables de ayudarme a resolver y explicar el siguiente ejercicio.
1 respuesta
Respuesta
1
La función es continua, por lo tanto si cambia de signo en los extremos del intervalo, entonces seguro tendrá una raíz en el mismo
f(1) = 1^3 + 4 * 1^2 - 8 = -3 < 0
f(2) = 2^3 + 4 * 2^2 - 8 = 16 > 0
Como es continua, la función tendrá una raíz en el intervalo
Lo voy a hacer en un XLS, ya que es un método iterativo...
Sean, 'a' y 'b' los extremos del intervalo y 'c' el punto medio del mismo...
El valor pintado de amarillo sería el valor de la raíz con el error aceptado de 10^(-4)
Salu2