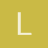¿No entiendo como el profesor sumo estos fasores?
El tema es así :
Tengo esta ecuación:
IR = IRS - ITR
IRS vale 18,26 y el angulo es -45.5º y es el fasor azul.,
Mientras que ITR vale 38.89 y esta a 213º y esta representado con un fasor violeta
Pero no entiendo porque extendió el fasor ITR del tercer cuadrante..., ¿al segundo cuadrante para sumarlos?
¿Y cómo determino que el angulo que coincide con la extensión del fasor es de 38º?
Espero alguien más entendido que yo me pueda explicar bien...
Gracias de antemano...
2 Respuestas
No lo está sumando sino restando... y para restar un vector de otro debes invertir el que restas y luego sumas. Normalmente.. Eso es lo que ha hecho tu profe. En símbolos IR= IRS +(- ITR).... Comprendes?... Además fíjate que 213,44 - 180 = 33.44... no se de donde obtienes los 38 grados...
Si... me equivoque .. no eran 38 º ... 38,8 es el valor del modulo ., lo que no entendía era como llego a los 33º-... ahora me doy cuenta resto los 213º que era la intentar original del fasor y le resto los 180º...
De modo que para restar un vector de otro ... primero debo invertirlo... no se que es invertir un fasor... si lo analizo..., ¿supongo qué invertir un fasor significa convertirlo en el fasor opuesto... o sea... eso significaría pasarlo al cuadrante opuesto no?
Pero analizando el ejercicio, para calcular las corrientes de línea, IR, IS e IT..., el profesor aplico la ley de nodos de kirchoff... o sea:
IR +ITR -IST = 0
IR = IST -ITR
cON ESTA FÓRMULA hallo IR..., pero supongo que el camino más fácil para hallar las corrientes de línea es multiplicar la corriente de fase por la raíz de 3
Pero yo calcule la IR multiplicando la corriente de fase IRS por raíz de 3
IR = IRS . 1,73
Pero el resultado no me coincide con el que resulta de aplicar la ecuación de kirchoff..., esto me deja intrigado ya que los resultados deberían coincidir tanto si aplicas un método como el otro...
¿No sabes por que no coinciden?
Ès que la relación V3 solo es válida para sistemas de fasores correspondientes a sistemas trifásicos balanceados. Lo que te dice el profesor es lo correcto.
;)
Es sencillo, pero primero valora la anterior pregunta:¿Cómo resuelvo este calculo con notaciones polares?
||*||
;)