De su gran apoyo para resolver por medio Sólidos de Revolución
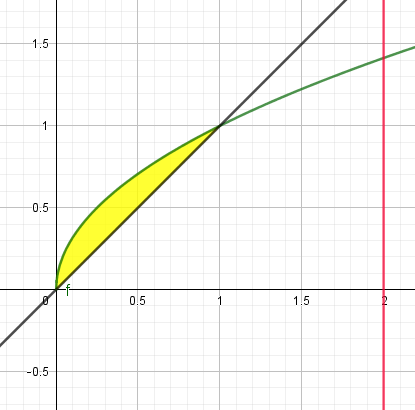
1. Construye la integral identificando puntos de corte, intervalo y su respectiva gráfica (mediante Geogebra) de los siguientes ejercicios.
2. Calcula el volumen del sólido al girar la región limitada por las curvas dadas alrededor del eje especificado y puedes comprobar mediante Geogebra:
1 respuesta
;)
Hola Elena!
Hacemos un problema de esos por pregunta.
Te hago el primero y manda el otro en otra pregunta o espera otro experto.
La zona que gira es:
Por el método de las arandelas o discos,
El volumen se calcula con la fórmula:
$$\begin{align}&V= \pi[Re(y)]^2-\pi[Ri(y)]^2\\&\\&R_e=radio\ exterior=2-f(y)\\&\\&r_i=radio\ interior=2-g(y)\\&\\&y= \sqrt x \ ==> x=y^2 ==>f(y)=y^2\\&\\&y=x ==> x=y ==> g(y)=y\\&\\&Puntos \ de \ corte\\&y^2=y\\&y^2-y=0\\&y(y-1)=0\\&y_1=0\\&y_2=1\\&\\&V=\pi \int_0^1 \Big[(2-y^2)^2-(2-y)^2 \Big]dy\\&\\&\pi \int_0^1 \Big[(4-4y^2+y^4)-(4-4y+y^2) \Big]dy=\\&\\&\pi \int_0^1 \Big(y^4-5y^2+4y \Big)dy=\\&\\&\pi \Bigg[ \frac{y^5}5 - \frac{5y^3}3+2y^2 \Bigg]_0^1=\\&\\&\pi( \frac 1 5- \frac 5 3+2)= \frac{ 8 \pi}{15}\end{align}$$Saludos y recuerda votar
;)
;)
||*||
;)
Buenas tardes profesor Lucas.
Usted utilizo las variables "y" es lo mismo si se utiliza la variable "x".
Saludos.
No es lo mismo,
Ya que al ser el eje de rotación vertical (x=2)
El radio lo mide la x, que es variable x=g(y)
En el otro problema que ahora te mando, gira alrededor de un eje horizontal, y los radios son y=f(x)
;)
