Teorema del valor medio problema a resolver dudas

Valor medio de la función en el intervalo que te están diciendo = Integral de la función dividido por el intervalo dado. El teorema del valor medio te dice que si la función es continua en un intervalo cerrado dado, por lo menos alcanza su valor medio al menos en un punto intermedio del intervalo.

Haces la integral:

Integral ( x^3 - 12x) dx entre -1 y 3 ...= /x^4 / 4 - 12 (x^2/2)/ definida entre -1 y 3 ... esta dandote ... -48.3... dividido ( 3-(-1)) = -12

Luego el valor promedio seria = -12

;)
Hola jerub!

Entiendo que sería el Teorema del Valor Medio, y no el Teorema del valor medio del calculo untegral o valor promedio. Como este ya lo hizo el profesor buscapolos, te hago el TVM

https://es.wikipedia.org/wiki/Teorema_del_valor_medio 

Que dice que si tiene una función continua y derivable en un intervalo, existe un punto (C) en dicho intervalo [-1,3] donde la pendiente de su recta tangente (f ' (C)) coincide con la pendiente de la recta

Que une los puntos extremos del intervalo (secante)

Recuerda que la pendiente de la tangente a una curva se calcula con la derivada.

Luego el Teorema asegura que encontraremos un punto en el intervalo donde:

$$\begin{align}&f'(C)=\frac{f(b)-f(a)}{b-a}\\&\\&Lo \ comprobamos:\\&pendiente\ de \ la \ secante:\\&\\&\frac{f(b)-f(a)}{b-a}=\frac{f(3)-f(-1)}{3-(-1)}=\\&\\&f(x)=x^3-12x\\&f(3)=27-36=-9\\&f(-1)=-1+12=11\\&\\&= \frac{-9-11}{4}=-5\\&\\&pendiente\ de º la \ tangente:\\&f'(x)=3x^2-12\\&\\&3x^2-12=-5\\&\\&x^2=\frac  7 3\\&\\&x= \pm \sqrt{\frac 7 3}\\&\\&x_1=1,5.......\\&x_2=-1.5......\\&\\&Donde \\&c=+ \sqrt{ \frac 7 3}\\&\end{align}$$

Como una imagen vale más que milpalabras:

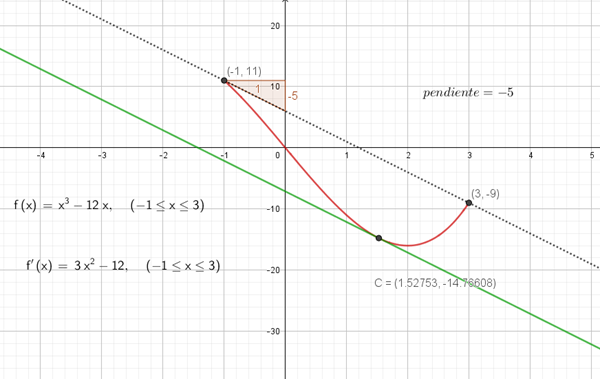
El punto C del intervalo cumple que la pendiente de la tangente ( recta verde) es igual a la pendiente de la secante ( recta punteada)

Como tienen la misma pendiente, esas dos rectas son paralelas.

En la práctica querría decir que como la velocidad es la derivada de la posición respecto el tiempo, y la posición de un automóvil varía de forma continua, si entre dos puntos que distan por ejemplo 100 km tardo 1 hora (velocidad media 100 km /h) este Teorema te asegura que por lo menos en un punto del recorrido llevo una velocidad de exactamente 100 km/h

Saludos y recuerda votar a todos los Expertos

Excelente para nuevas respuestas mías

;)

||*||

;)