;)
Hola Yani!
b)
z=f(x,y)
Las curvas de nivel salen de dar un valor constante (k) a la función z
f(x,y)=z= k
$$\begin{align}&\cos^2(x^2+y^2)=k\\&\\&\text{como el \cos }\alpha \text{está comprendido entre -1 y 1}\\&\\&-1 \leq \cos(x^2+y^2) \leq1 \Rightarrow\\&\\&0 \leq \cos^2(x^2+y^2) \leq 1 \Rightarrow\\&\\&0 \leq k \leq 1\\&\\&0\leq x^2+y^2 \leq 2 \pi\end{align}$$Las curvas de nivel son circunferencias centradas en el origen, excepto para k=1 que es el Origen de coordenadas. Asi:
$$\begin{align}&k=0 \Rightarrow \cos^2(x^2+y^2)=0 \Rightarrow \cos(x^2+y^2)=0 \Rightarrow\\& x^2+y^2= \frac \pi 2\\&\\&x^2+y^2= \frac {3 \pi} 2\\&\\&k= \frac 1 2 \Rightarrow \cos^2(x^2+y^2)=\frac 1 2 \Rightarrow \cos(x^2+y^2)= \pm \frac{\sqrt 2} 2 \Rightarrow \\&x^2+y^2= \frac \pi 4\\&\\&x^2+y^2= \frac {3 \pi} {4}\\&\\&x^2+y^2= \frac{5 \pi }{4}\\&\\&x^2+y^2= \frac{7 \pi} 4\\&\\&k=1 \Rightarrow \cos^2(x^2+y^2)=1 \Rightarrow \cos(x^2+y^2)=\pm 1 \Rightarrow \\&x^2+y^2=0 \ (\text{origen de coordenadas})\\&\\&x^2+y^2=\pi\\&\\&\\&\end{align}$$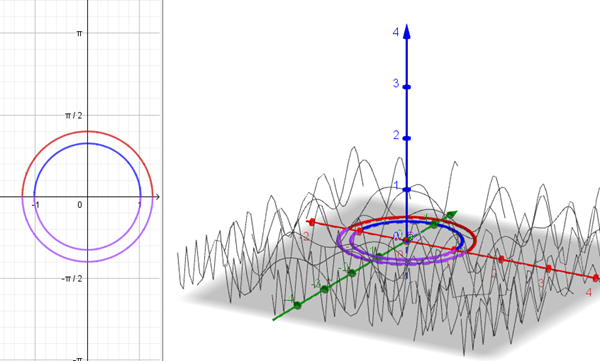
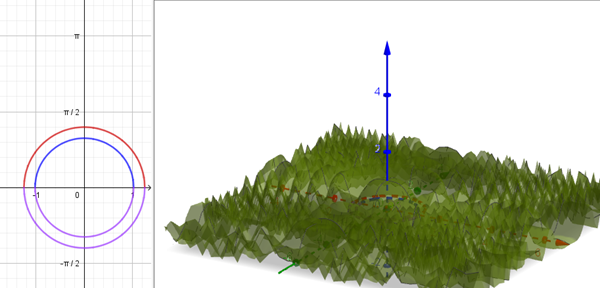
Saludos
;)
;)



