Hallar la solución de la siguiente inecuación racional y comprobar su solución con Geogebra.(x^2-9)/(x^2-25)≤0

Tenemos que ver los ceros de la función y los puntos donde la función es discontinua, esto definirá una serie de intervalos donde la función será continua (ya que salvo en los puntos en que es discontinua, se tratan de polinomios que siempre son continuas)

$$\begin{align}&\frac{x^2-9}{x^2-25}\le0\\&\frac{(x-3)(x+3)}{(x-5)(x+5)}\le0\\&\text{Por lo que los puntos donde la función se anula o vale 0, son }\{-5,-3,3,5\}\\&\text{que define los intervalos:} (-\infty, -5), (-5, -3), (-3,+3), (+3, +5),(+5,+\infty)\\&\text{En cada intervalo voy a evaluar el signo de la función, para ver si cumple o no con la condición}\\&(-\infty, -5) \to x=-10 \to f(-10)=\frac{(-10-3)(-10+3)}{(-10-5)(-10+5)}=\frac{(-)(-)}{(-)(-)}=\frac{+}{+}>0 \to NO!\\&(-5, -3)\to x=-4 \to f(-4)=\frac{(-4-3)(-4+3)}{(-4-5)(-4+5)}=\frac{(-)(-)}{(-)(+)}=\frac{+}{-}<0 \to Cumple!\\&(-3,+3)\to x=0 \to f(0)=\frac{(0-3)(0+3)}{(0-5)(0+5)}=\frac{(-)(+)}{(-)(+)}=\frac{-}{-}>0 \to NO!\\&(+3, +5)\to x=4 \to f(4)=\frac{(4-3)(4+3)}{(4-5)(4+5)}=\frac{(+)(+)}{(-)(+)}=\frac{+}{-}<0 \to Cumple!\\&(+5,+\infty)\to x=10 \to f(10)=\frac{(10-3)(10+3)}{(10-5)(10+5)}=\frac{(+)(+)}{(+)(+)}=\frac{+}{+}>0 \to NO!\\&\text{Por lo que las soluciones buscadas son }\\&x \in (-5, -3) \cup (+3, +5)\end{align}$$

Te dejo el gráfico de la función

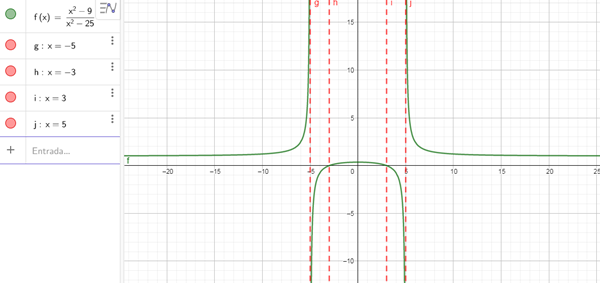
Salu2