¿Cómo se puede resolver el siguiente ejercicio?
El área de un rectángulo es igual a 48 m2. Las distancias de un punto de la base a los vértices opuestos a la misma miden 13m y 4m. Calcular la base del rectángulo.
2 respuestas
Respuesta de javicl
2
Un desarrollo magnífico.
Con permiso me gustaría completar y sugerir.
Habría que descartar la solución cuadrática ya que en ese caso z sale negativo. Con lo cual la única medida posible de la base es 15.
Como sugerencia os animo a que volváis a plantearlo pero a partir de la Fórmula de Herón en el triangulo de la figura.
Respuesta de Lucas m
1
$$\begin{align}&48=xy\\&\\&Pitágoras PHS\\&13^2=y^2+(x-z)^2\\&\\&Pitágoras \ RHQ\\&\\&4^2=z^2+y^2\\&\\&Restandoº las \ dos \ últimas\\&169-16=(x-z)^2-z^2\\&\\&153= x^2-2xz+z^2-z^2\\&\\&153=x^2-2xz ==> z=\frac{x^2-153}{2x}\\&\\&Sustituyendo \ en \ la \ segunda:\\&y^2=16-z^2=16- \frac{x^4-306x^2+23409}{4x^2}= \frac{64x^2-x^4+306x^2-23409}{4x^2}\\&\\&y= \frac 1 {2x} \sqrt{64x^2-x^4+306x^2-23409}\\&\\&y= \frac 1 {2x} \sqrt{-x^4+370x^2-23409}\\&\\&sustituyendo º en \ la \ primera\\&48=xy\\&\\&48= \frac 1 2 \sqrt{-x^4+370x^2-23409}\\&\\&96=\sqrt{-x^4+370x^2-23409}\\&\\&elevandoº al\ cuadrado\\&\\&9216={-x^4+370x^2-23409}\\&\\&x^4-370x^2+32625=0\\&\\&ecuación\ bicuadrada\\&x^2=t\\&t^2-370t+32625=0\\&\\&t_1=225 ==> x_1=15 \ ===>\ y_1=\frac{48}{15}= \frac {16} 5=3,2\\&\\&t_2=145\ ===> x_2= \sqrt{145} \ ==> \ y_2= \frac{48}{145}\\&\end{align}$$;)
Hola Sofía!!
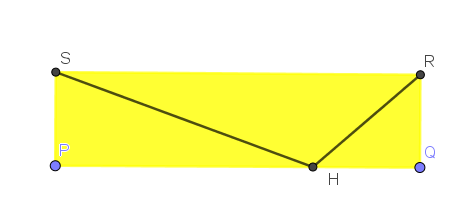
PQ=x
QR=y HQ=z PH=x-z SH=13 HR=4
Area:
$$\begin{align}&48=xy\\&\\&Pitágoras PHS\\&13^2=y^2+(x-z)^2\\&\\&Pitágoras \ RHQ\\&\\&4^2=z^2+y^2\\&\\&Restandoº las \ dos \ últimas\\&169-16=(x-z)^2-z^2\\&\\&153= x^2-2xz+z^2-z^2\\&\\&153=x^2-2xz ==> z=\frac{x^2-153}{2x}\\&\\&Sustituyendo \ en \ la \ segunda:\\&y^2=16-z^2=16- \frac{x^4-306x^2+23409}{4x^2}= \frac{64x^2-x^4+306x^2-23409}{4x^2}\\&\\&y= \frac 1 {2x} \sqrt{64x^2-x^4+306x^2-23409}\\&\\&y= \frac 1 {2x} \sqrt{-x^4+370x^2-23409}\\&\\&sustituyendo º en \ la \ primera\\&48=xy\\&\\&48= \frac 1 2 \sqrt{-x^4+370x^2-23409}\\&\\&96=\sqrt{-x^4+370x^2-23409}\\&\\&elevandoº al\ cuadrado\\&\\&9216={-x^4+370x^2-23409}\\&\\&x^4-370x^2+32625=0\\&\\&ecuación\ bicuadrada\\&x^2=t\\&t^2-370t+32625=0\\&\\&t_1=225 ==> x_1=15 \ ===>\ y_1=\frac{48}{15}= \frac {16} 5=3,2\\&\\&t_2=145\ ===> x_2= \sqrt{145} \ ==> \ y_2= \frac{48}{145}\\&\end{align}$$Saludos
;)
||*||
Muchas gracias!!
Una consulta
Porque desarrollaste dos veces?
;)
Fue un error de la página
;)
||*||
;)