¿Cuántas personas se registraron al taller de música?
En un centro cultural que oferta talleres se inscribieron 90 personas. 59 se registraron a música o arte pero no ambas. 57 se han registrado a danza o a música, pero no ambas. 14 se registraron a danza y arte. 12 se registraron a arte y música. 13 se registraron a música y danza. 4 personas tomarán los tres talleres
El problema por el que da negativo es que algunas ecuaciones no están correctamente planteadas.
(a + f)+(b+e) = 59
(a + d)+(c+e) = 57
e + g= 14
d + g= 12
f +g = 13
g = 4
a + b + c + d + e + f + g = 90
Lo resuelves y el universo hace su trabajo.
Salu2.
¡Gracias! profe. Javicl. agradezco tu observación y corrección, ahora me pondré a trabajar, le envió saludos cordiales.
1 respuesta más de otro experto
Primero vamos a hacer el esquema general
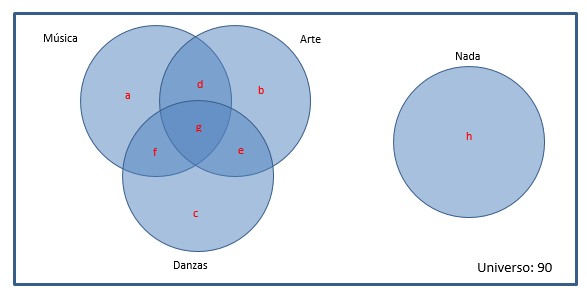
Además de los datos que sabemos tenemos que:
a + b = 59
a + c = 57
e = 14
d = 12
f = 13
g = 4
Además podemos considerar que h=0 (ya que no tiene sentido que una persona se inscribió a la escuela pero a ningún taller) y el caso general:
a + b + c + d + e + f + g = 90
Rescribamos la última ecuación con los datos conocidos...
a + b + c + 12 + 14 + 13 + 4 = 90
a + b + c = 47
Y ahora tenemos 3 ecuaciones con 3 incógnitas (a,b,c). Lo puedes resolver por el método que quieras, en particular voy a usar lo que conocemos de las 2 primeras ecuaciones y remplazarlo en esta última expresión hallada
(a + b) + c = 47
59 + c = 47 --> c = -12
b + (a + c) = 47
b + 57 = 47 --> b = -10
a + b + c = 47 --> a - 10 - 12 = 47 --> a = 69
La solución está completa, pero el problema es que tu profesor no validó que los resultados sea coherentes, ya que según estos resultados, el resultado de solo arte y solo danza es negativo, cosa que más allá que matemáticamente sea posible, obviamente no tiene un sentido en la realidad.
Más allá del "detalle" anterior, en función a los datos obtenidos la respuesta es que al taller de música asistieron a + d + f + g = 69 + 12 + 13 + 4 = 98 (por supuesto que este resultado es absurdo, ya que solo había 90 personas inscriptas, pero esto pasa por los valores negativos obtenidos antes)...
Salu2
Himelda, tiene razón javicl respecto a las fórmulas a considerar, creo que entre esa correción más lo que inicialmente te había planteado podrás llegar a la solución, en caso que no sea así avisa donde te quedan dudas.
Salu2
¡Gracias! profe. Gustavo voy a checar , pero con lo planteado ya puedo trabajar la actividad. en verdad agradezco su valioso apoyo.
saludos cordiales