Problema de sistemas de ecuaciones de porcentajes
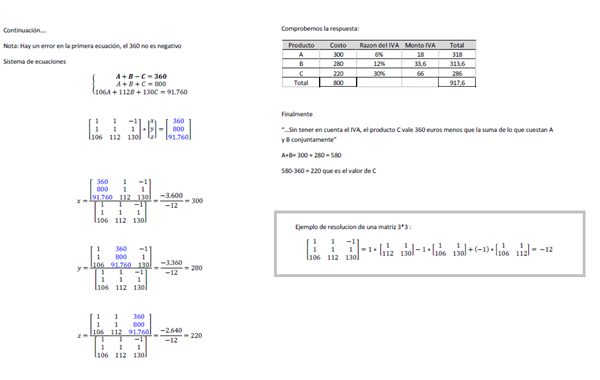
Se han comprado tres productos A, B y C. Sin tener en cuenta el IVA, el producto C vale 360 euros menos que la suma de lo que cuestan A y B conjuntamente, mientras que el importe total de los tres productos asciende a 800 euros. El producto A paga un IVA del 6%, el producto B del 12% y el producto C del 30. La factura total con IVA importa 917.60 euros.
- Plantear un sistema de ecuaciones para calcular la cantidad, sin IVA, que cuesta cada producto.
- Resolver el sistema por Cramer.
1 respuesta
Respuesta de Hiroshi Kurosawa
1