Como hallar la ecuación canónica de una circunferencia
¿Me pueden ayudar con este ejercicio?
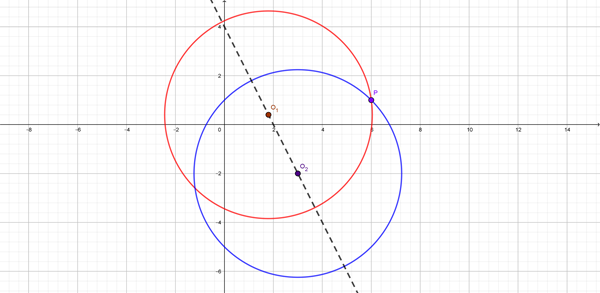
Hallar la ecuación canónica de una circunferencia de radio √18, pasa por el punto (6,1) y su centro es un punto de la recta Y = 4-2X
1 respuesta
Respuesta de Karl Mat
1