Anónimo
¿Esta bien planteada así la serie?
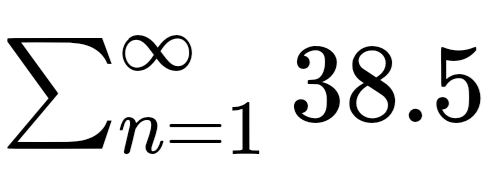
La química es el componente activo del medicamento que se usa para tratar la malaria. Se sabe que pasadas las 24 horas de ingerida una dosis de quinina sólo el 23% la cantidad original permanece ej el organismo.
Supongamos que una persona ingiere una dosis de 50mg de química tofos los días a la misma hora. Sea Sn la cantifad de quinina en el organismo de dicha persona en el día. Calcular sn y el limite
Sn lo calcule así como la imagen. Quería saber si está bien. Y ahora como se calcula el límite.
1 Respuesta
En el día 1 tiene 50mg.
En el día 2 tiene 0.23·50 (del día anterior) + 50mg nuevos. Total: 61.5
En el día 3 tiene 0.23·(50+0.23·50) = 0.23^2·50 + 0.23·50 del día anterior +50mg nuevos. Total: 64.145
En el día 4 tiene 0.23^3·50 + 0.23^2·50 + 0.23·50 del día anterior +50mg nuevos. Total: 64.75335
La serie es (cantidad en el día k)
$$\begin{align}&\sum_{n=1}^k 0.23^{n-1} \cdot 50 \end{align}$$Quieres calcular el límite cuando k tiende a infinito.
Sea la sucesión
$$\begin{align}&a_n = 0.23^{n-1}\cdot 50\end{align}$$Entonces el límite de la serie anterior es
$$\begin{align}&\sum_{n=1}^\infty 0.23^{n-1} \cdot 50 = \sum_{n=1}^\infty a_n\end{align}$$Como a(n) es una sucesión geométrica con razón r = 0.23, siendo 0 < r < 1, entonces la suma de los infinitos términos es
$$\begin{align}&\sum_{n=1}^\infty a_n = \frac{a_1}{1-r} =\\&= \frac{50}{1-0.23} = \frac{5000}{77} \simeq 64.9351 \end{align}$$