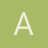Anónimo
Esta bien resuelto el ejercicio de limites?
$$\begin{align}&\\&\lim _{x\to +\infty \:}\left(\frac{4x^4-2x^3+x^2+4x+2}{3x^4-3x^3+7x^2+x+1}\right)\\&\\&\lim _{x\to+ \infty \:}\left(\frac{4-\frac{2}{x}+\frac{1}{x^2}+\frac{4}{x^3}+\frac{2}{x^4}}{3-\frac{3}{x}+\frac{7}{x^2}+\frac{1}{x^3}+\frac{1}{x^4}}\right)\\&\\&\frac{\lim _{x\to +\infty \:}\left(4-\frac{2}{x}+\frac{1}{x^2}+\frac{4}{x^3}+\frac{2}{x^4}\right)}{\lim _{x\to+ \infty \:}\left(3-\frac{3}{x}+\frac{7}{x^2}+\frac{1}{x^3}+\frac{1}{x^4}\right)}\\&\\&\\&\\&4/3\\&\\&\end{align}$$Quiero saber si esta bien resuelto este ejercicio pide hallar el limite. No se si es lo mismo calcular el limite como +infinito=infinito
2 Respuestas
Respuesta de Andrés L.
Es correcto.
No es necesario hacer tantos cálculos: hay un regla para los límites de cocientes de polinomios según los grados de los polinomios. En este caso, como tienen el mismo grado, el resultado del límite es el cociente de los coeficientes directores.
Respuesta
Está perfecto resuelto (si recién estás empezando con los límites de polinomios). Una vez que tengas un tiempo haciendo ejercicio verás que
$$\begin{align}&\lim_{x \to \infty} \frac{P(x)}{Q(x)} = \\&Si\ Gr(P(x)) > Gr(Q(x)) \to \infty\\&Si\ Gr(P(x)) < Gr(Q(x)) \to 0\\&Si\ Gr(P(x)) = Gr(Q(x)) \to \frac{a}{b}...\text{donde a es el coeficiente principal de P(x) y b el}\\&\text{coeficiente principal de Q(x)}\\&\\&\end{align}$$Salu2