Como resuelvo el siguiente problema de trigonométrica

;)

Es imposible que te dé, sin el proceso!

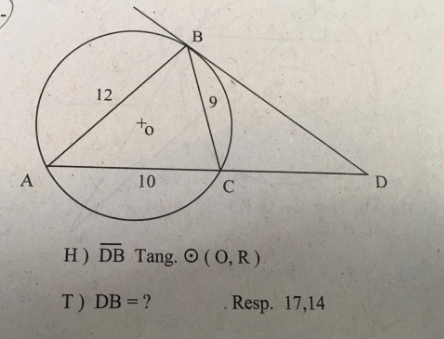
Con el Teorema del coseno, puedes calcular los tres ángulos del triángulo:

a^2=b^2+c^2-2bc cosA.  ==>

cos A=(b^2+c^2-a^2)/(2bc)=

(10^2+12^2-9^2)/(2•10•12)=0.6791

A=arccos0.6791=47.22°

b^2=a^2+c^2-2ac cosB

cosB=(a^2+c^2-b^2)/(2ac)=

(9^2+12^2-10^2)/(2•9•12)=0.578

B=arccosB=54.64°

C=180°-A-B=78.14

Aplicamos el Teorema del seno en el triángulo ABD:

BD/sinA =12/sinD

BD=12• sinA/sinD=

Hemos de calcular el ángulo D:

ángulo CBD es semiinscrito y abarca el mismo arco que el ángulo A , luego son iguales ==> angCBD=42.22°

angBCD=180°-C=180°-78.14=101.86

Luego en el triángulo BCD==>

D=180°-42.22°-101.86°=35.92

BD=12• sinA/sinD=12•sin47.22/sin35.92=

17.14

Repasa los cálculos

;)