Cuanto Vale la Integral Doble

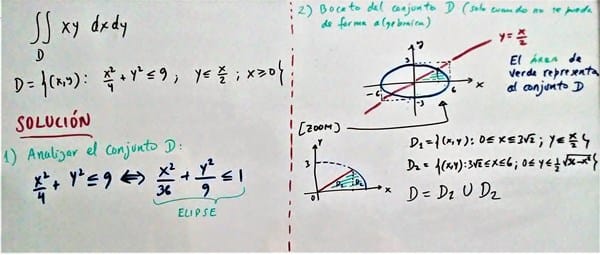
Ahora calcularemos a integral

$$\begin{align}&I=\iint\limits_Dx+y~dx~dy\\&\\&I=\iint\limits_{D_1}x+y~dx~dy+\iint\limits_{D_2}x+y~dx~dy\\&\\&I=\int\limits_{0}^{3\sqrt2}\int\limits_{0}^{x/2}x+y~dy~dx+\int\limits_{3\sqrt2}^{6}\int\limits_{0}^{\frac{1}{2}\sqrt{36-x^2}}x+y~dy~dx\\&\\&I=\int\limits_{0}^{3\sqrt2}\left.\left(xy+\dfrac{y^2}{2}\right)\right|_{y=0}^{y=x/2}dx+\int\limits_{3\sqrt2}^{6}\left.\left(xy+\dfrac{y^2}{2}\right)\right|_{y=0}^{y=\frac{1}{2}\sqrt{36-x^2}}dx\\&\\&I=\int\limits_{0}^{3\sqrt2}\dfrac{x^2}{2}+\dfrac{x^3}{8} dx+\int\limits_{3\sqrt2}^{6}\frac{x}{2}\sqrt{36-x^2}+\frac{36-x^2}{4}dx\\&\\&I=\left.\dfrac{x^3}{6}+\dfrac{x^4}{32}\right|_{0}^{3\sqrt2}+\left.\left(-\frac{1}{6}\sqrt{36-x^2}^3+9x-\frac{x^3}{12}\right)\right|_{3\sqrt2}^{6}\\&\\&I=\frac{369}{8}-\frac{9\sqrt2}{2}\end{align}$$