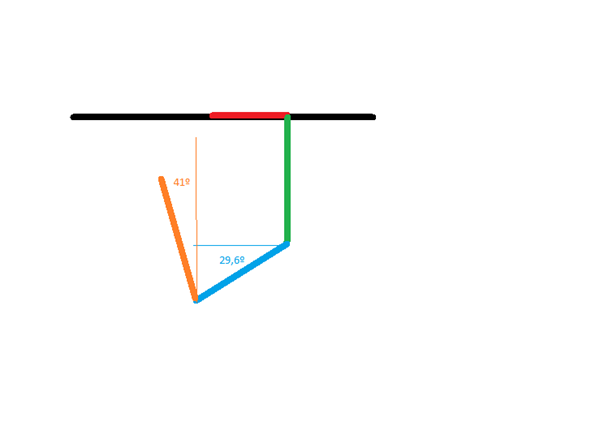
Este seria el movimiento que tienen los estudiantes, mas o menos, no está a escala pero para darnos una idea está bien.
Ahora sobre los vectores unitarios, estamos en un movimiento bidimiensional, los vectores unitarios son el i para el eje x y el j para el eje y. Lo que te piden es representar los vectores como la suma de las componentes x e y
Ahora recuerda que;
$$\begin{align}&componente \ x: rcos\phi\\&componente \ y: rsen\phi\end{align}$$Ahora el primer vector dice que se mueve al este, es decir el angulo es cero.
V1= 1,02x10^3 cos0 i+1,02x10^3sen0 j= 1,02x10^3 i (que concuerda con lo que dice que va a la derecha, ya que solo tiene componente i, es decir en x)
El segundo vector va hacia el sur, que son 270°
v2=2,15x10^3cos270 i+2,15x10^3sen270 j=-2,15x10^3 j
El tercer vector dice que va al sur del oeste 29,6°. Esta es un poco mas tramposa, el oeste son 180° pero bajas 29,6° mas, es decir 209,6°
V3=3,45x10^3 cos209, 6 i + 3,45x10^3 sen209, 6 j =-3x10^3 i -1,7x10^3 j (Quiero que notes que los signos concuerdan, recuerda en un eje cartesiano en el primer cuadrante ambos valores son positivos, en el segundo x es negativo, en el tercero ambos son negativos y en el cuarto y es negativo. Ese vector que va hacia abajo del oeste si se posiciona en el origen se esta dirigiendo hacia el tercer cuadrante, por lo que los dos valores deben dar negativo, que nos dio asi)
El cuarto vector nos dice que se movió al oeste del norte, es decir, a la izquierda del norte. El norte es 90° mas 41° que se movió, el angulo es de 131 . (Que hubiera pasado si dijera que se movia al este del norte, es decir a la derecha del norte, pues que al norte le restas 41, no le sumas)
v4=4,01x10^3cos131 i +4,01x10^3 sen131 j=-2,63x10^3+3,03x10^3
Organizando
v1=1,02x10^3 i+0j
v2=0i-2,15x10^3 j
v3=-3x10^3 i -1,7x10^3 j
v4=-2,63x10^3+3,03x10^3
b) Hay que sumar los vectores, para hallar el vector resultante, es sumar las i con las i, y las j con j
Vt=-4,61x10^3 i -0.82x10^3 j (De aqui puedes interpretar que si el origen es donde comenzaron, ellos se encuentran en el tercer cuadrante, muy alejados horizontalmente pero no tanto verticalmente)
c) Para que lleguen al origen al vector total hay que hallar un vector que sumado al vector resultante de cero. Es sencillo, el 4,61x10^3 i +0.82x10^3 j. Solo se cambia de signo. Ahora para hallar la distancia hay que hallar el modulo del vector que es
$$\begin{align}&\sqrt{(4,61x10^3)^2+(0,82x10^3)^2}=4,67x10^3m\end{align}$$y el angulo es
$$\begin{align}&tg \phi=\frac{x}{y}=\frac{4.61x10^3}{0.82x10^3}\\&\phi=79,91°\end{align}$$d) El dibujo te lo dejo a ti, de hecho es bastante parecido al que hice, no es exactamente igual por si acaso.
e) Es solo sumar las distancias que nos da el ejercicio



