Encuentre un z3 tal que los puntos z1, z2, z3 forman un triángulo equilátero

Para que sea equilatero la distancia (d) entre los 3 puntos debe ser la misma, o sea

d(z1,z2) = d(z2,z3) = d(z3,z1)

$$\begin{align}&d(z_1,z_2) = \sqrt{(2-(-2))^2+(2-(-2))^2}=\sqrt{32}\\&Sea\ z_3=a+bi\\&d(z_2,z_3)=\sqrt{(-2-a)^2+(-2-b)^2}=\sqrt{a^2+b^2+4(2+a+b)}\\&d(z_1,z_3)=\sqrt{(2-a)^2+(2-b)^2}=\sqrt{a^2+b^2+4(2-a-b)}\\&\text{Ahora usamos las igualdades entre los 3 puntos}\\&\sqrt{a^2+b^2+4(2+a+b)} = \sqrt{32}\\&\sqrt{a^2+b^2+4(2-a-b)} = \sqrt{32}\\&\text{Elevo todo al cuadrado}\\&{a^2+b^2+4(2+a+b)} = {32}          .....(*)\\&{a^2+b^2+4(2-a-b)} = {32}\\&\text{Resto ambas expresiones}\\&2a+2b=0 \to a+b=0 \to a=-b\\&\text{Reemplazo eso en las expresiones (*)}\\&(-b)^2+b^2+4(2-b+b)=32\\&2b^2+8=32\\&b^2 = 12\\&b = \sqrt{12}\\&b = \pm 2 \sqrt{3} \to a = \mp 2 \sqrt{3}\end{align}$$

Es lógico que sean dos los puntos posibles. La imagen sería:

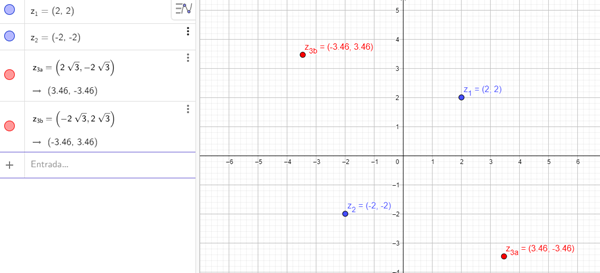
Salu2