Se solicita calcular el siguiente límite al infinito y comprobar en GeoGebra que el límite existe,y el desarrollo analitico
- Calcular el siguiente límite al infinito y comprobar en GeoGebra que el límite existe, presentar la gráfica de donde se evidencie la existencia del límite y el paso a paso del desarrollo analítico del ejercicio.
$$\begin{align}&〖lim┬(x→∞) 〗〖√(x^2+6x+7)/√(3x^2+4)〗\end{align}$$
2 Respuestas
El trabajo 'pesado' ya lo hizo albert, así que acá dejo el gráfico y las verificaciones de lo que él hizo está bien
$$\begin{align}&Nota:\ recuerda\ que\\&\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}3 \approx 0.58\end{align}$$
No me manejo con GeoGebra. Te adelanto que el límite existe porque la función así presentada tiende a un valor finito distinto de cero.
El numerador, para valores de x suficientemente grandes el termino x^2 supera cuanto desees al resto, y puede aproximarse a Vx^2
El denominador, para valores de x suficientemente grandes pasa lo mismo con el termino en x^2 y puede aproximarse a V3x^2
Luego tendiendo x a infinito la expresión que te están dando tenderá a Vx^2 / V3x^2 o sea = 1 / V3,
La tendencia es por ambos lados (-infinito) a ( + infinito) y la funcion será real y continua salvo un reducido intervalo central en que se hace imaginaria.
El gráfico por GeoGebra te mostraria bien todo y tal vez te lo pueda aportar algun otro colega, a quien invito a participar.
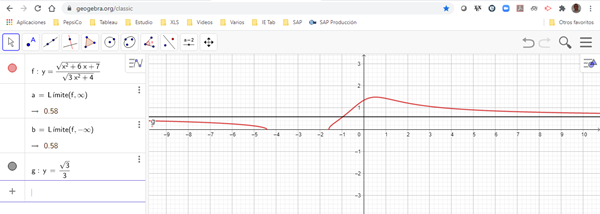
Es una función " jodida" porque toma todo el eje x salvo un reducido sector en que se hace imaginaria verdad Gustavo? - albert buscapolos Ing°