Ecuación f(x) = 2x2-6x + 4 con un puntoinicial p = 3 con un error de

Esa ecuación la podrías hallar de manera exacta, pero supongo que estás viendo temas de aproximación, punto fijo y Newton-Rapson.

Justamente este último método, cuando converge es un método excelente por su velocidad, lo que tienes que tener es la función (que te la dieron), la derivada (que es fácil de calcular) y un punto inicial (que también te lo dieron).

Calculemos la derivada

f'(x) = 4x - 6

y las aproximaciones se consiguen calculando los puntos

$$\begin{align}&x_{i+1}=x_i- \frac{f(x_i)}{f'(x_i)}\\&Cuando \ x_{i+1} - x_i < \text{ Error buscado, finaliza el enunciado y }x_{i+1} \text{ es la solución}\end{align}$$

Lo que sigue lo voy a hacer en una tabla en excel por su sencillez

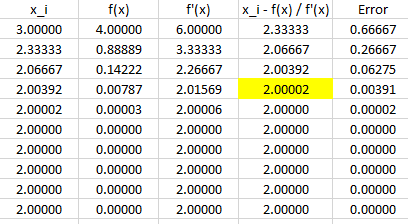
Realicé las 10 iteraciones que te pidieron y marqué la solución basados en el error que te piden (aunque claramente la solución exacta para este problema es x=2)

Salu2