La verdad no entendi muy bien estos ejercicios
Agradecería si me ayudaran por que la verdad no entiendo nada
2 respuestas
Respuesta de albert buscapolos Ing°
Te resuelvo dos ya que es norma responder uno por vez.
a) ...............Y=/X-2/ + 1 el recorrido seria una V con vertice en el punto { 2, 1 }
b) ... Y = V( 6x-5) el recorrido esta definido solo para (6x - 5 )> 0 ...... x > -5/6 seria una semiparabola.
En la primer ecuación la V tendría pendiente de 45° a la derecha y 135° a la izquierda.
Respuesta de Dante Amor
Te ayudo con el ejercicio D
Lo que debes encontrar es el recorrido de la función, es decir, los valores que puede tomar la función en el eje de las y
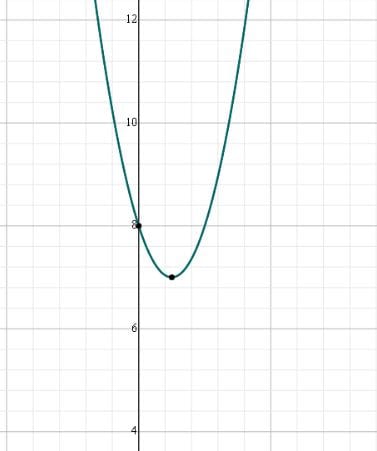
$$\begin{align}&o(x)=(2x-1)^2+7\\&es\ lo\ mismo\\&y=(2x-1)^2+7\\&\\&Función\ inversa\\&y = (2x -1) * (2x - 1) + 7\\&y = 4x^2 - 2x - 2x + 1 + 7\\&y = 4x^2 - 4x + 8\\&4x^2 - 4x + 8 -y = 0\\&\\&Paralelistmo\ con\ la\ forma:\\&ax^2 + bx + c = 0\\&Entonces:\\&a = 4\\&b = -4\\&c = (8 -y)\\&\\&fórmula\ general\\&x = \frac{-b \frac{+}{-}\sqrt{b^2 -4ac}}{2a}\\&x = \frac{-(-4) \frac{+}{-}\sqrt{-4^2 -(4)(4)(8-y)}}{2(4)}\\&x = \frac{4 \frac{+}{-}\sqrt{16 -128+16y}}{8}\\&\\&Debemos\ encontrar\ el\ número\ que\ está\ dentro\ de\ la\ la\ raíz\ sea\ mayor\ o\ igual\ cero\\&en\ esta\ ecuación:\\&16 -128+16y\\&Despejamos\ y\\&16y -112 = 0\\&16y = 112\\&y = 112 / 16\\&y = 7\\&\\&o(x) \ge 7\\&Recorrido\ [7, \infty )\\&\end{align}$$Lo anterior significa que o(x) puede tomar valores desde el 7 positivo hasta el infinito.
La gráfica:
Revisa lo siguiente para entender qué es el recorrido y qué es el dominio: