Hallar la distancia más corta entre las dos rectas que se cruzan
hallar la distancia mas corta entre las dos rectas que se cruzan x+y+2z-1=0,x-2y-z-1=0 y 2x-y+z-3=0,x+y+z-1=0
1 Respuesta
Respuesta
1
Si dos rectas se cruzan, entonces la distancia más corta será justamente donde se cortan (y esa distancia será 0). Para eso debes igualar ambas rectas.
Igualmente vos no estás dando dos rectas, sino que estás dando dos planos que se cortarán en una recta (salvo que los planos sean paralelos).
$$\begin{align}&Sea\ P=(x_0,y_0,z_0) / P \in R1 \land P \in R2\\&Recta 1:\\& x+y+2z-1=0\\&x-2y-z-1=0\\&Resto:\\&3y+3z=0\\&Si\ P \in R1 \to y_0=-z_0\\&Recta 2:\\&2x-y+z-3=0\\&x+y+z-1=0\\&Sumo:\\&3x+2z-4=0\\&Si\ P \in R2 \to x_0=\frac{-2z_0+4}{3}\\&P=(\frac{-2z_0+4}{3},-z_0,z_0) = z_0(-\frac{2}3,-1,1) + (\frac{4}3,0,0)\\&\text{O sea que la recta definida por los planos dados es:}\\&L = \lambda (-\frac{2}3,-1,1) + (\frac{4}3,0,0)\end{align}$$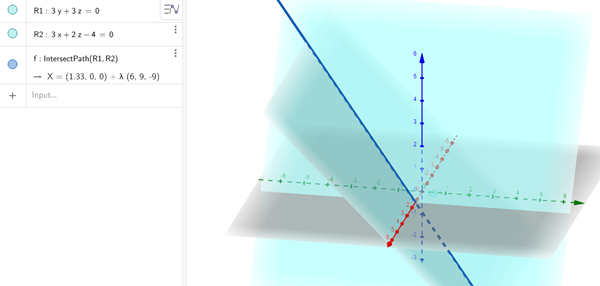
Te dejo la imagen con la solución en Geogebra, donde el vector director es distinto al que puse yo, pero claramente se ve son múltiplos entre ambos