Hallar los respectivos datos de las siguientes ecuaciones

Te resuelvo el F (el B no lo veo bien en la imagen y la idea es hacer solo un ejercicio de este tipo por preguntas ya que, como ves, son de una extensión bastante considerable)

$$\begin{align}&y = \sqrt{\frac{x+1}{x-2}}\\&Dominio: \\&\text{Como tenemos una raiz par, debe ser donde el interior sea positiva, además como }\\&\text{hay una fracción, debe ser donde el denominador no sea 0}\\&x-2 \ne 0 \to x \ne 2\\&\frac{x+1}{x-2} \ge0\\&\text{Como tenemos una fracción, para que sea positiva, ambos términos deben tener el mismo signo}\\&\text{Encontramos los puntos de interés para x = {-1, 2} que son los que anulan numerador o denominador}\\&\text{que es donde la función puede cambiar de signo, así que analizamos el signo de la función en los intervalos}\\&(-\infty, -1) \text{ voy a usar x=-2} \to \frac{-2+1}{-2-2} =\frac{-1}{-4}=+ \text{solo importa el signo}\\&(-, 2) \text{ voy a usar x=0} \to \frac{0+1}{0-2} =\frac{+1}{-2}=- \text{solo importa el signo}\\&(2, +\infty) \text{ voy a usar x=3} \to \frac{3+1}{3-2} =\frac{4}{+1}=+ \text{solo importa el signo}\\&\text{Además en x=-1 la función vale 0, por lo que la raiz también está definida, en conclusión}\\&Dominio: (-\infty, 1] \cup (2, +\infty)\\&\\&\text{Intersección con los ejes (para esto hay que ver cuando x=0 (intersección con eje Y) y cuando y=0 (intersección con eje X)}\\&\text{x=0 no tiene sentido, ya que no forma parte del dominio}\\&X:\\&0 = \sqrt{\frac{x+1}{x-2}}...\\&x=-1\\&\\&\text{Recorrido: (no sé como lo haces tu, yo lo que hago es calcular la inversa de la función y ver su dominio)}\\&y = \sqrt{\frac{x+1}{x-2}}\\&y^2={\frac{x+1}{x-2}}\\&y^2(x-2)=x+1\\&y^2x-2y^2=x+1\\&y^2x-x=1+2y^2\\&x(y^2-1)=1+2y^2\\&x=\frac{1+2y^2}{y^2-1}\\&\text{Ya tenemos la fórmula de la inversa, por lo que el rango (recorrido) es donde no está definida esta nueva función}\\&Recorrido: R \ne {\pm 1}\\&\text{Positividad: Es una raíz cuadrada, por lo tanto siempre que esté definida será positiva (salvo donde vale 0)}\\&Asíntotas:\\&Vertical: x=2\\&Horizontal: \text{esta asociado a lo que vimos de la función inversa...}\end{align}$$

Te ayudo con el g) - pero no dejes de puntuarnos -

Determine las intersecciones con los ejes coordenados,

La función solo tiene soluciones reales para x> -5 porque sino la raíz ( x+5) se haría imaginaria, Para x< -5 no existe.

La intersección con el eje x solo se da en el eje x positivo, igualando la función a 0. Obtenés x(0) = 2.69.

Para determinar las intersecciones con el eje "y" te conviene separar los trozos a ambos lados de la indeterminación. ( x= +2). Y analizas cada lado.

Con el eje x ...........intersecta solamente en x= 2.69..................( haces y=0), 

Con el eje y ............intersecta en y = 1.11  .....................( haces x= 0 en la ecuacion).

Dominio y recorrido,

Para -5 < x la funcion no existe en el campo real.

Para x>= -5 <2  la funcion esta definida para los valores  comprendidos entre  f(-5)  y + infinito.

Para 2 < x < + infinito la funcion dada esta comprendida entre - infinito y un valor asintotico = 1 que luego definiremos.

Ecuaciones de las asíntotas,

Hay una sola asíntota horizontal, que la podes deducir haciendo limites.

Y asintota = lim x --> infinito ( +) de la funcion original = x - (x+5)^0.5 / ( x-2) 

Para x muy grande puede aproximarse mas y mas a 1 + (1/ Vx )-que ----> 1 con x tendiendo a infinito.

Asintota horizontal : y= 1

Asintota vertical :  x= 2

intervalos de positividad,

Positiva entre -5 >=x< 2    y    x > 2.69 

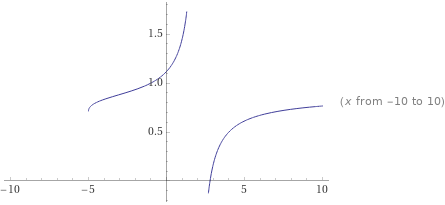
Te paso la grafica: