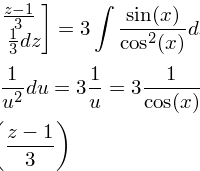carolina2511

canalrev respondió: Con los datos que das no es un triángulo isósceles, sino rectángulo, donde la hipotenusa mide (x^2+a^2)^(1/2) y los catetos x y a El problema es de cual de, los dos ángulos que no son rectos hay que hallar las razones trigonométricas. Supongo que es...

canalrev respondió: 1) 8x^2/((x+1)^2(x-3))=(9/2)/(x-3)-1/(x+1)^2 +(7/2)/(x+1) int 8x^2 dx =int (9/2)/(x-3) dx - int 1/(x+1)^2 dx + int (7/2)/(x+1) dx = (x+1)^2(x-3) 9/2 · ln(x-3) +2/(x+1) + 7/2 · ln(x+1) +c 2) senx/(cos^2 x+5cosx+6)=senx·(1/(cosx+2) -...

canalrev respondió: 1) int sen((z-1)/3) dz cos^2((z-1)/3) hacemos el cambio t=cos((z-1)/3) dt=sen((z-1)/3)/3 int sen((z-1)/3) dz = int dz = -1 +c = -1 +c cos^2((z-1)/3) 3·t^2 3t 3·cos((z-1)/3) 2) int sen (x)ln cos(x) dx hacemos el cambio t=cos (x) dt=-sen(x) int sen...

Fran José García respondió: Te dejo una imagen con la solución de la primera si no ves la imagen dimelo Cualquier paso que no entiendas preguntame

Fran José García respondió: Bueno aquí antes de hacer el cambio de variable (sustitución) vamos a operar un poco Sabemos que sec(y) = 1/cos(y) y que tan(y) = sen(y)/cos(y) entonces la función nos queda (1+sen(y))^4/(1/cos(y) + sen(y)/cos(y)) = cos(y) (1+sen(y))^4/(1+sen(y)) =...

Fran José García respondió: Bueno para aplicar esto vamos a aplicar partes para ello consideramos u = e^x || du = e^xdx dv = x/(x+1)^2||v = 1/(x+1)+log(x+1) Para calcular v = hemos calculado la integral de x / (x+1)^2, que se calcula por partes, es sencilla su resolución...

Fran José García respondió: Bueno aquí escogemos el siguiente cambio de variable u = 2y+1 entonces du = 2 dy entonces la integral nos queda (1/2)?1/u^(1/2)du = (1/2) 2 u^(1/2), si deshacemos el cambio y simplificamos el (1/2) con el 2, nos queda u^(1/2) = (2y+1)^(1/2)

Fran José García respondió: Bueno para integrar por partes vamos a considerar las variables u y dv para elegir la "u" vamos a aplicar lo que podemos llamar la regla de los ALPES A: Aquí significa todos los arcos, es decir, arcos, arcsen, arctg. L: Logaritmos P: Polinomios E:...

Fran José García respondió: En la primer aplicamos partes y la regla de los alpes que te dije en la otra respuesta Entonces u = Ln(x)||du = 1/x dx dv = 1/x^2||v = -1/x entonces la intergral ?ln(x)/x^2dx = - ln(x)/x + ?1/x^2dx = -ln(x)/x - 1/x Ahora te pongo la otra