Resuelve los siguientes problemas de máximos y mínimos, así como su representación gráfica de una

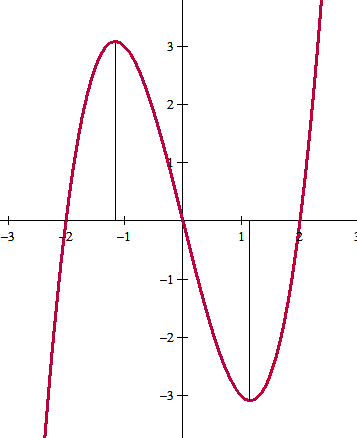
La función es un polinomio, luego está definido en todo R, es continua y no tiene asíntotas. Tiene simetría central por ser todos los términos impares con lo cual f(-x) = -f(x)
Los cortes con el eje X son
x^3-4x = 0
x(x^2-4) = 0
x = 0, -2 y 2
y el corte con el eje Y es y =0
La derivada primera es
f '(x) = 3x^2 -4
Los punto críticos son
3x^2 =4
x^2 = 4/3
x = - 2/sqrt(3) y 2/sqrt(3)

En (-oo, -2/sqrt(3)) es f '(x) positiva luego la función crece
en(-2/sqrt(3), 2/sqrt(3)) por ejemplo en 0 f'(0) = -4 es negativa luego la función decrece
Y en (2/sqrt(3), oo) es positiva como lo prueba el hecho que el limite en +oo es +oo luego la función crece.

La derivada segunda es
f ''(x) = 6x
En -2/sqrt(3) es f ''(x) negativa. Luego es un máximo

El valor del máximo es

f(x)=x^3-4x = -8/[3·sqrt(3)] + 8/sqrt(3) =

(-8 +24) /[3·sqrt(3)] = 16/[3·sqrt(3)] = 3.079201436

El máximo aproximado escrito en decimal para que podamos representarlo es

(-1.1547, 3.0792)

Y en 2/sqrt(3) es f ''(x) positiva, luego es un mínimo Y por simetría central el mínimo es

(-1.1547, -3.0792)

f''(x) es negativa en (-oo, 0) luego la función es cóncava hacia abajo.
Y f''(x) es positiva en (0, oo) luego la función es cóncava hacia arriba.

Y esta es la gráfica.

Y eso es todo.