Pues vamos a encontrar la ecuación correcta de la hipérbola.
La parte de calcular los vértices de la elipse es igual y se llega a
V1 = (11, 3)
V2 = (5, 3)
Ahora cambiamos algo.
El centro de la hipérbola es la intersección de las asíntotas
4x-3y-23=0
4x+3y-41=0
Las sumamos
8x - 64 = 0
x = 8
32 - 3y - 23 =0
3y=9
y=3
Luego el centro de la hipérbola es (8,3)
Al ser el centro (8,3) y pasar la hipérbola por los puntos simétricos V1(11, 3) y V3(5, 3), estando los tres en horizontal, significa que el eje longitudinal es paralelo al eje X, ya que de los ejes longitudinal y perpendicular que pasan por el centro, el longitudinal es el que corta a dos puntos simétricos de la hipérbola y el perpendicular no corta a ninguno
Entonces tenemos que la hipérbola será de la forma
$$\begin{align}&\frac{(x-8)^2}{a^2}-\frac{(y-3)^2}{b^2}=1\\ &\end{align}$$Y las asíntotas serán
$$\begin{align}&y=3\pm \frac ba(x-8)\\ &\\ &\text {las que nos dan son}\\ &\\ &4x-3y-23=0\\ &4x+3y-41=0\\ &\\ &\text{que puestas en la forma de arriba son}\\ &\\ &y=\frac 43x-\frac{23}{3}=3+\frac 43(x-8)\\ &y=-\frac 43x+\frac{41}{3}=3-\frac 43(x-8)\\ &\\ &\text{luego igualando se obtiene }\frac ba=\frac 43\\ &\end{align}$$a=3b/4
la otra vez lo puse al reves.
Y la ecuación de la hipérbola será
$$\begin{align}&\frac{(x-8)^2}{\left(\frac{3b}{4}\right)^2}-\frac{(y-3)^2}{b^2}=1\\ &\\ &\text {para que pase por }V_1(11,3)\\ &\\ &\frac{(11-8)^2}{\left(\frac{3b}{4}\right)^2}-\frac{(3-3)^2}{b^2}=1\\ &\\ &\frac{9}{\frac{9b^2}{16}}=1\\ &\\ &\frac{16}{b^2}=1\\ &\\ &b=4\\ &a=3·4/4=3\end{align}$$Luego la ecuación es
$$\begin{align}&\frac{(x-8)^2}{3^2}-\frac{(y-3)^2}{4^2}=1\\ &\end{align}$$Esta es la gráfica.
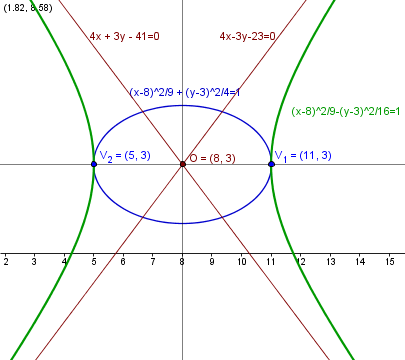
Antes podía tener razón el profe en que la respuesta estaba mal, pero era un hiperboal de todas maneras, no una circunferencia como decía.
Y eso es todo, es un ejercicio que te puedes liar. Y sobre todo lo que me falta a mi es que no tengo un libro de referencia sobre esto, no hago masque buscar y buscar artículos según necesito una cosa concreta y no encuentro el que diga todo lo necesario.


