Sacar volumen de prisma

Pues no es un problema nada fácil. Existe la fórmula de Herón que nos da al área de un triángulo conociendo los lados.

Fórmula de Herón

$$\begin{align}&Área=\sqrt{s(s-a)(s-b)(s-c)}\\ &\\ &\text{donde s es el semiperímetro}\\ &\\ &s=\frac{30+70+60}{2}=80cm \\ &\\ &Área=\sqrt{80(80-30)(80-70)(80-60)}=\\ &\\ &\sqrt{80·50·10·20}=\sqrt{800000}=894.427191 cm^2\\ &\\ &Volumen =500·894.427191 =447213.5955cm^3\\ &\\ &\text {O podemos expresarlo de otras formas}\\ &\\ &447.213\;litros\\ &0.447213m^3\end{align}$$

Lo que se ha usado es que el volumen de un prisma es el área de la base multiplicada por la altura, ponemos el prisma de pie y la base será el triángulo.

Lo normal es que no conozcas la fórmula de Herón, deducir el área del triángulo sin ella es para sudar algo.

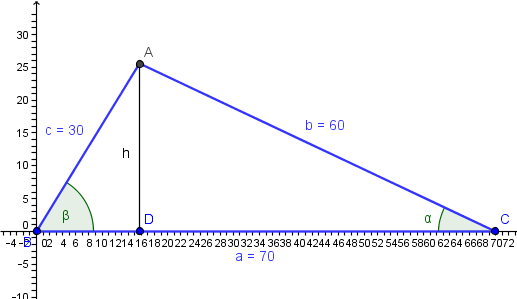
La altura será

h=30sen(beta) ==> cos(beta) = sqrt[1 - (h/30)^2]

h=60sen(alfa) ==> cos(alfa) = sqrt[1- (h/60)^2]

la base del triángulo es

30cos(beta)+60cos(alfa) = 70

$$\begin{align}&30 \sqrt{1-\frac{h^2}{900}}+60 \sqrt{1-\frac{h^2}{3600}}= 70\\ &\\ &\\ &900-h^2+3600-h^2 +2 \sqrt{900-h^2}\sqrt{3600-h^2}=4900\\ &\\ &\\ &2 \sqrt{900-h^2}\sqrt{3600-h^2}=400+2h^2\\ &\\ &4(900-h^2)(3600-h^2)= 160000+4h^4+1600h^2\\ &\\ &12960000 -18000h^2+4h^4 = 160000+4h^4+1600h^2\\ &\\ &19600h^2 =12800000\\ &\\ &h^2=\frac{12800000}{19600} =\frac{32000}{49}\\ &\\ &h = \frac{80 \sqrt 5}{7}\\ &\\ &Area\; triángulo = \frac{70·\frac{80 \sqrt 5}{7}}{2}=400 \sqrt 5 \approx 894.427191\\ &\\ &\end{align}$$

Bien, como puedes ver hemos llegado a la misma área del triángulo que con la fórmula de Herón pero usando argumentos trigonométricos asequibles.

Y el volumen es el que ya calculamos al principio.

Y eso es todo.