¿Buenas me podrías ayudar en este problema de calculo integral?
es de sólidos de revolución dice asi:
la región limitada por el primer cuadrante,por la curva y=lnx y por la recta que pasa por (0,1) que es tangente a dicha curva, gira alrededor del eje y,calcular el volumen del solido generado, de antemano muchas gracias,
1 respuesta
No es nada sencillo.
Las rectas tangentes a la función en un punto son
y = yo + f '(xo)(x-xo)
ln'(xo) = 1/xo
y = yo + (x-xo) / xo
y la que pasa por (0, 1) será
1 = ln(xo) +(0-xo)/xo
1 = ln(x0) -1
ln(xo) = 2
xo = e^2
Luego la recta es
y = 2 + (x-e^2)/e^2 = 1+ x/e^2
Este es el gráfico, la zona de color es la que genera el objeto al girar sobre el eje Y
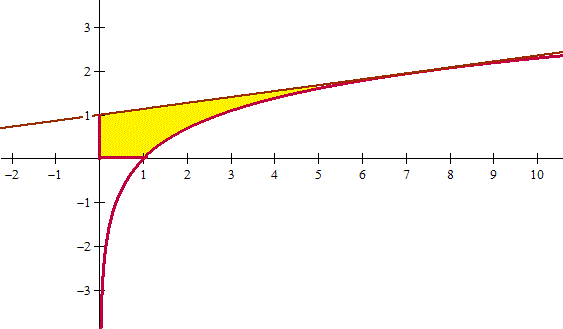
Por girar sobre el eje Y debemos poner la x como función de y
y = lnx ==> x = e^y
y = 1+x/e^2 ==> x = (y-1)e^2
El volumen será el engendrado por la curva
x=e^y
menos el generado por la recta
x =(y-1)e^2
que es interior al de la curva
Los límites se tienen que calcular en y.
Arriba calculamos que el punto xo donde era tangente la recta era
xo=e^2
luego el valor de y es
y = ln(e^2) = 2
Luego los limites en y de la curva x?e^y son 0 y 2
Y la recta x=(y-1e^2) tiene los límites 1 y 2. El 2 por coincidir con la curva y el 1 porque no s decían que pasaba por ahí.
El volumen de la curva entre y=0 y y=2 es
$$\begin{align}&V_c=\pi\int_0^2[f(y)]^2dy =\\ &\\ &\pi\int_0^2e^{2y}dy =\frac {\pi}2\left[e^{2y}\right]_0^2=\\ &\\ &\frac {\pi}2(e^4-1)\\ &\\ &\\ &\\ &\\ &V_r=\pi\int_1^2(y-1)^2e^4dy=\\ &\\ &e^4\pi \left[\frac{y^3}{3}-y^2+y \right]_1^2=\\ &\\ &\\ &e^4\pi\left(\frac 83-4+2-\frac 13+1-1 \right)=\\ &\\ &\\ &e^4\pi\left(\frac 73-2 \right)=\frac{e^4\pi}{3}\\ &\\ &\\ &\text{Y el volumen pedido es}\\ &\\ &\\ &V=V_c-V_r=\frac {\pi}2(e^4-1)-\frac{e^4\pi}{3}=\\ &\\ &\frac{\pi e^4}{6}-\frac{\pi}{2}\approx 27.01672818 u^3\end{align}$$Y eso es todo.
porque restas los volumenes?
Cuando calculas el volumen generado por la curva calculas el volumen del cuerpo solido que tiene altura 2, todo lo que genera la curva al girar desde la base 0 hasta la altura 2 es lo que he llamado Vc. Pero la figura que se genera tiene un hueco por arriba que es precisamente el que genera al girar la recta entre la altura 1 del centro y la altura 2 por el exterior. Ese volumen que está hueco es el que se calcula con la integral Vr. Luego si al volumen de todo le restamos el volumen del hueco ese, queda exactamente el volumen de la figura coloreada al girar.
Fíjate que sería algo parecido a un plato. Con la primera integral calculas el volumen del plato lleno, con la segunda el de la sopa y restando del total el de la sopa tienes el volumen del plato.
