Integrales convergentes o divergentes
Tengo que averiguar si la siguiente integral es convergente o divergente y también hallar su valor.
Tengo entendido que si el resultado me da uno es convergente y si me da infinito es divergente. Corrígeme si me equivoco.
Creo que la resolución seria mediante la integración y luego hacer su limite, pero no se dicho limite a que tendría que tender.
¿Cómo se resolvería?
Valero angel serrano tienes malo el limite cuando x tiende a 2 por izquierda del ln(x-2) ya que como se puede observar que en al evaluar en dos por izquierda en x-2 queda negatio entonces cuando evalúas en el Ln de un numero negativo no existe.
En mi opinión ya que la hice a mano y no se si estará mala o buena aunque ya la he revisado varias veces es convergente esa área de la función y es un Lnl4/3l evaluando la función en 2 y en 1 obteniendo este resultado. Por favor revisar bien si estoy mal yo o esta mal valero o estamos mal los dos.
1 respuesta más de otro experto
En x=2 la función se hace infinita y no se puede evaluar la integral definida mediante la regla de Barrow. Es por eso que debe calcularse el límite de la integral definida cuando x -->2-.
Si el limite existe y es finito se dice que la integral es convergente. Si es infinito se dice que es divergente. Luego cualquier valor finito del límite sirve, no solo el 1 como decías.
Se puede calcular la primitiva y luego hacer el límite. Lo que pasa es que es a veces es difícil calcular la primitiva o simplemente queremos saber solo si es convergente o no. Y para ello existen unos criterios de comparación con otras funciones que no sé si los habrás dado ya.
El criterio de Pringsheim nos dice que esta integral es divergente:
Sea f una función no negativa localmente integrable en el intervalo [a, b) con -oo<a<b<oo y tal que para algún a existe el limite
lim x-->b- de (b-x)^a·f(x) = L € [0,+oo)U{+oo}
entonces
- si a>=1 y L>0 la integral de f entre a y b diverge a +oo
- si a<1 y L distinto de +oo la integral de f entre a y b converge
En nuestro caso tomamos a =1
lim x -->2- de (2-x)(x+1)/(4-x^2) =
lim x -->2- de (2-x)(x+1)/[(2-x)(2+x)] =
lim x-->2- de (x+1)/(2+x) = 3/4
Y como a>=1 y L>0 diverge.
Sin utilizar el criterio también se puede hacer pero como ya te decía puede costar algo resolver, yo la resuelvo con un programa aunque es bastante sencilla y se puede hacer a mano.
$[(x+1)/(4-x^2)]dx =-(1/4)[ln(x+2)+3*ln(x-2)]
Y el límite cuando x-->2-
Es
-(1/4)[ln(4)+3ln(0)] =(-1/4)[ln(4)-oo] = -(1/4)(-oo) = +oo divergente
Y eso es todo.
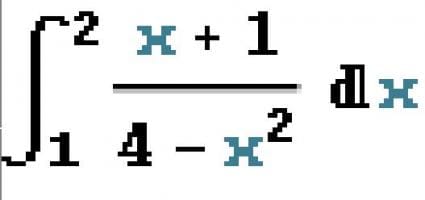
Soy Valero. Muchas veces nos resistimos a ponerlo, pero en las integrales que da un logaritmo hay que poner el logaritmo del módulo. Por lo tanto la integral verdadera es -(1/4)[ln|x+2| + 3*ln|x-2|] Ahora ya no se da el caso de inexistencia del límite y el resultado final es el que ya había puesto. - tmoli