Ayuda urgente. Geometría anailitica I
Buenas tardes. Ojala me puedas ayudar. Saludos.
Problema. El puente
Se desea construir un puente peatonal en forma de elipse para cruzar una carretera muy transitada.
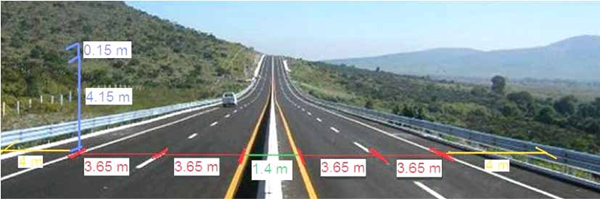
Se sabe que la carretera tiene 4 carriles, 2 en un sentido y 2 en otro, y una separación de 1 metro entre los carriles de ida y los de vuelta. Por esta carretera, en el carril de baja velocidad, circularán tráilers, los cuales tienen una altura máxima permitida de 4.15 metros, por lo que se ha decidido dejar 15 cm más de altura, justamente en la línea de acotamiento, como medida de seguridad para que éstos puedan circular libremente. Por las dimensiones del terreno se desea que los extremos del puente estén situados a 2 metros de distancia de donde inicia la línea de acotamiento de la carretera.
Con la información que tiene, el arquitecto ha propuesto el siguiente esquema: