Hallar mínima distancia entre 2 funciones

La correspondencia y^2=x se compone de dos funciones

y = sqrt(x)

y = -sqrt(x)

Donde sqrt es la raíz cuadrada.

Nada más que hagas la gráfica verás que es la primera de las dos funciones la más cercana a la recta y = x+1.

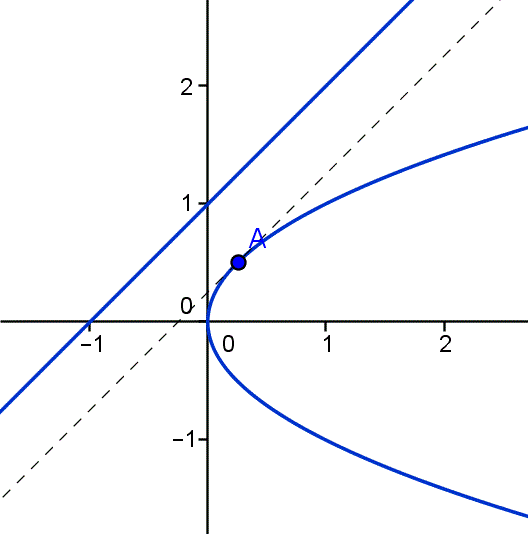
Luego podemos limitar el problema a hallar la distancia más corta entre las funciones

y=sqrt(x)

y = x+1

Me juego lo que quieras a que la distancia más corta es la que hay entre el punto de la función sqrt(x) que tiene la tangente paralela a la recta y la recta.

Lo hago de esta manera y luego lo hacemos con máximos y mínimos si quieres, pero va a dar lo mismo y será más complicado.

Derivamos sqrt(x) para hallar el punto con derivada 1, lo mismo que la pendiente de la recta

sqrt'(x) = 1/(2sqrt(x))

Lo igualamos a 1

1/(2sqrt(x)) = 1

2sqrt(x) = 1

sqrt(x) = 1/2

x = 1/4

Luego el punto más cercano será:

(1/4, 1/2)

Y la distancia a la recta es aplicando la fórmula de la distancia punto a recta:

|y-x-1|/sqrt(2) = |1/2 - 1/4 -1| / sqrt(2) =|(2-1-4)/4|/ sqrt(2) = 3/[4sqrt(2)] =

(3/8) sqrt(2) = 0.5303300859

Ese es el método más sencillo. Espero que te sirva y lo hayas entendido. NO olvides puntuar.

Si quieres que lo haga con teoría de máximos y mínimos, que ahora mismo no lo he meditado del todo, pero creo que no son necesarios los multiplicadores de Lagrange, mándame de nuevo el problema en una pregunta nueva tras puntuar esta. Me haces experto favorito y así te será más sencillo mandármela directamente.