Representar la gráfica de una función

El dominio es todos los puntos salvo los que anulan el denominador

3x-x^2 = 0

x(3-x) = 0

x=0

x=3

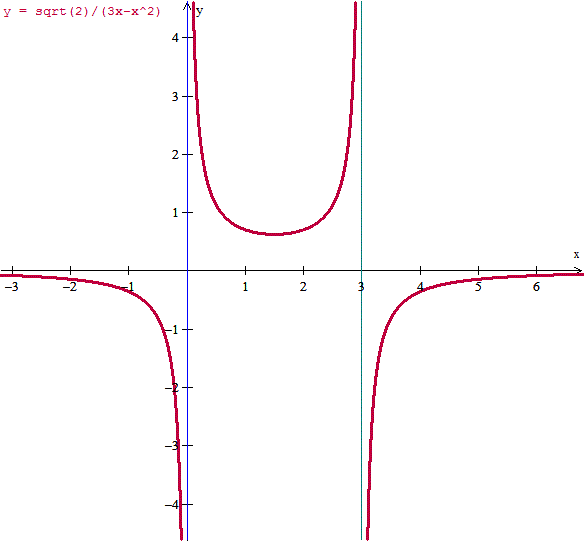
Dom f = R - {0, 3}

Cortes con el eje X no puede haber ya que nunca puede valer y=0

Corte con el eje Y tampoco porque en x=0 no está definida la función

Los signo de la función depende del signo del denominador que ya calculamos que era cero en x=0 y x=3

En (-oo, 0) en -1 por ejemplo f(-1) = -3-1 = -4 es negativa

En (0,3) en x=1 por ejemplo f(1) = 3-1 = 2 es positiva

En (3,+oo) en x=4 por ejemplo f(4) = 12-16 = -4 es negativa

Hay asíntotas verticales en x=0 y x=3 porque el limite es infinito es esos puntos.

Hay asíntototas horizontales porque el límite en +-oo es 0. La asíntota es y=0

No hay asíntotas oblicuas por hay horizontales

La derivada primera es

f '(x) = sqrt(2)·(-3+2x) / (3x-x^2)^2

se anula en x=3/2 y no está definida en 0 y 3

En (-oo, 0) es f '(-1) = (-3-2)/(algo positivo) es negativa luego decrece f(x)

En (0, 3/2) es f '(1) = (-3+2)/(positivo) es negativa luego drecrece f(x)

En (3/2, 3) es f '(2) = (-3+4)/(positivo) es positiva luego crece f(x)

en (3,+oo) es f '(4) = (-3+8)/(positivo) es positiva luegro crece f(x)

En el punto x=3/2 pasa de decrecer a crecer luego es un mínimo relativo. El valor en el mínimo es

f(3/2) = sqrt(2) / (9/2 - 9/4) = sqrt(2) / (9/4) = 4·sqrt(2)/9

Luego el mínimo es (3/2, 4·sqrt(2)/9)

Para hacernos una idea es (1.5, 0.6285)

Es bastante difícil calcular el signo de la derivada segunda, no creo que te lo pidan

$$\begin{align}&f´´(x)=\sqrt 2 \left(\frac{2(3x-x^2)^2-(-3+2x)2(3x-x^2)(3-2x)}{(3x-x^2)^4}\right)\\ &\\ &\end{align}$$

Nos guiaremos por otras cosas como que la función es derivable salvo en 0 y 3, entonces el mínimo tendra forma de U.

La función tiene el signo de x(3-x) luego en 0- tiene límite -oo y en 0+ es +oo. Y en 3- es +oo y en 3+ es -oo

Y con ests cosas y algún punto si es necesario se dibuja la función.

Y eso es todo.