De todos los conos que pueden inscribirse en una esfera...
De todos los conos que pueden inscribirse en una esfera de radio 12, calcular el que tiene volumen máximo.
El cono tocará la esfera por la punta y por la circunferencia de la base. Si hacemos un corte con un plano que corte el cono exactamente por la mitad tendremos la figura de un triángulo inscrito en una circunferencia.
El volumen del cono es:
V = Pi·r^2·h/3
Cuidado, con r nos referiremos al radio de la base del cono, no al radio de la esfera.
En el triangulo del plano de corte, la base será 2r y la altura h.
Dado un triángulo inscrito en una circunferencia y dada la base fija, el triángulo que más altura tiene es el isósceles. Para comprobarlo traza una cuerda paralela al eje X por debajo de este, y el triángulo se completará con un punto de la circunferencia. La altura será la distancia del punto a esa cuerda, y la máxima distancia está en el punto de arriba de la circunferencia que origina un triángulo isósceles. Luego dado un r que hace de base, podremos obtener mas h y por tanto más volumen si construimos el triangulo isósceles tal como tenemos en la figura.
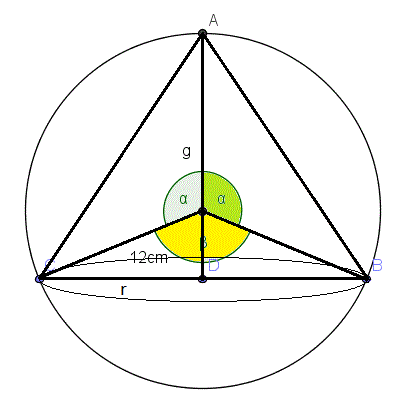
Vamos a hallar r^2 en función de h
h=12+12sen[(180º-beta)/2] ==> sen[(180º-beta)/2] = (h-12)/12
b = 2r = 2·12·cos[(180º-beta)/2] ==> cos[(180º-beta)/2 = r/12
Sabemos que sen^2(x)+cos^2(x) = 1 luego
(h-12)^2/12^2 + r^2/12^2 = 1
h^2 + 144 - 24h + r^2 = 144
r^2 = 24h - h^2
Y tenemos el volumen del cono solo en función de h
V = Pi· (24h^2 - h^3)/3
Derivamos e igualamos a cero para hallar el máximo respecto a h
V '(h) = (Pi/3)(48h - 3h^2) = 0
48h - 3h^2 = 0
16h = h^2
h = 16
La derivada segunda es
V ''(h) = (Pi/3)(48-6h)
V ''(16) = (Pi/3)(48-96) < 0 luego es un máximo
y ahora calculamos r
r^2 = 24·16 - 16^2 = 128
r =sqrt(128) = 8sqrt(2) = 11,313708
Pues ya lo tenemos, el como inscrito de mayor tamaño es el que tiene altura 16 y radio 8sqrt(2)
Y eso es todo.
