Ejercicio Matrices Columna
La pregunta es la siguiente:
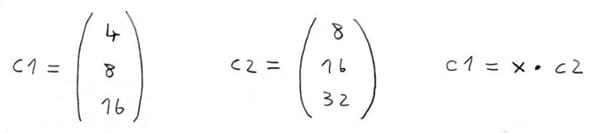
A simple vista se ve que si son proporcionales y que el valor seria x=2.
Mi duda esta en como se resolvería esa ecuación aislando la x de las matrices??.
Como en principio no se pueden dividir matrices yo había pensado en desarrollar esto mediante la matriz identidad:
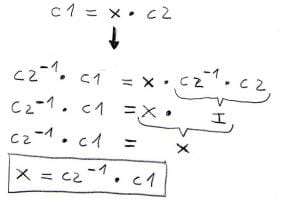
pero me he encontrado con que para calcular la matriz inversa de C2 hay que sacar su matriz adjunta transpuesta dividido su determinante y en estas matrices que no son cuadradas y no se hacerlo.
Gracias por anticipado.
1 respuesta
Es que las matrices que no son cuadradas no tienen inversa. Una matriz inversa es la inversa de una aplicación lineal de un espacio vectorial en sí mismo, y esas aplicaciones lineales de un espacio en si mismo tienen una matriz cuadrada como representación. Tampoco tienen determinante si no son cuadradas-
Lo que si se puede hacer es multiplicar adecuadamente por alguna matriz para despejar la x
Toma una matriz A no nula de dimensiones 1x3 y multiplícala a la izquierda en ambos lados, así conseguirás que se reduzca todo a números
| 4|
(a1, a2, a3) · | 8| = 4a1 + 8a2 + 16a3
|16|
| 8|
(a1,a2,a3) · x · |16| = x(8a1 + 16a2 + 32a3)
|32|Luego
4a1 + 8a2 + 16a3 = x (8a1 + 16a2 + 32a3)
Y suponiendo que 8a1 + 16a2 + 32a3 es distinto de cero tenemos
x = (4a1 + 8a2 + 16a3) / (8a1 + 16a2 + 32a3) = 1/2
Por cierto, era x = 1/2 no 2.
Es mucho más sencillo en la practica, basta que tomes la matriz (1,0,0) y te queda
4 = 8x
x = 1/2
Y eso es todo.
Gracias, ya lo he entendido, simplemente 2 preguntas:
1.- ¿Cuando dices una matriz no nula te refieres solamente a que al menos uno de sus términos no sea un cero?
2.- ¿Y en el caso de que las matrices que me da el enunciado si fueran cuadradas el método que yo había planteado seria correcto y podría llegar a la solución mediante el?
1. Si, una matriz no nula es una que tiene al menos un elemento distinto de cero, solo con que sea uno ya sirve. Aparte de que A no fuera nula tenía que darse también que A·c1 sea distinto de cero. Si por casualidad te salía alguna asi prueba con otra.
2) Si, si son cuadradas se puede emplear el método ese. Pero úsalo con cuidado, lo primero tienes multiplicar siempre por la izquierda o siempre por la derecha, porque el producto de matrices no es conmutativo en general.
Y también hay casos en que no existirá la inversa, cuando el determinante sea 0, luego habrá que saber que la matriz no tiene determinante 0 para poder aplicar la inversa.
Eso es todo.
