a)
Este problema veo que va a resultar muy difícil de entender sin un dibujo
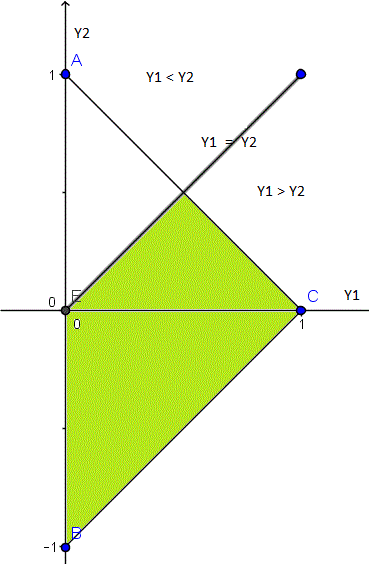
El triángulo ABC es la zona donde la probabilidad no es nula. La recta Y1=Y2 divide el plano en dos zonas, una donde Y1 < Y2 que es la superior y otro done Y1> y2 que es la inferior y de la que nos piden la probabilidad, luego la P(Y1>Y2) es la de la zona de verde.
A través del dibujo vemos que tiene dos limites superiores distintos:
Si 0 <= Y1 <= 1/2 ==> Y1-1 <= Y2 <= Y1
Si -1/2 <= Y1 <= 1 ==> Y1-1 <= Y2 <= 1-Y1
Se me olvidó poner en el dibujo que la recta BC es Y2= Y1-1 y que la recta AC es Y2=1-Y1 para que hubiera sido completamente claro
Bueno, pues esos dos limites que hemos calculado habrá que integraros en dos integrales:
$$\begin{align}&P(Y_1\gt Y_2)= \\ &\int_0^{\frac 12}\int_{y_1-1}^{y_1} 30y_1y_2^2dy_2dy_1 + \int_{\frac 12}^1\int_{y_1-1}^{1-y_1} 30y_1y_2^2dy_2dy_1=\\ &\\ &\\ &\int_0^{\frac 12}10y_1[y_2^3]_{y_1-1}^{y_1}dy_1+\int_{\frac 12}^1 10y_1[y_2^3]_{y_1-1}^{1-y_1}dy_1=\\ &\\ &\int_0^{\frac 12}10y_1(y_1^3-y_1^3 +3y_1^2-3y_1+1) dy_1 +\\ &\\ &\int_{\frac 12}^{1}10y_1(1-3y_1+3y_1^2-y_1^3-y_1^3+3y_1^2-3y_1+1)dy_1 =\\ &\\ &\\ &10\int_0^{\frac 12} (3y_1^3- 3y_1^2+y_1)dy_1+\\ &10\int_{\frac 12}^1(2y_1-6y_1^2+6y_1^3-2y_1^4)dy_1=\\ &\\ &\\ &\\ &10\left[\frac {3y_1^4}{4}-y_1^3+\frac {y_1^2}{2} \right]_0^{\frac 12}+ 10\left[y_1^2-2y_1^3+\frac {6y_1^4}{4} -\frac {2y_1^5}{5} \right]_{1/2}^1=\\ &\\ &10\left(\frac{3}{64}-\frac 18+\frac 18+1-2+\frac 64-\frac 25-\frac 14 +\frac 28-\frac {6}{64}+\frac{2}{160} \right)=\\ &\\ &\\ &10\left(\frac{-3}{64}+\frac 28-1+ \frac 54- \frac 25+ \frac{1}{80}\right)=\\ &\\ &10\left(\frac{-3+16-64+80}{64}-\frac{32-1}{80} \right)=\\ &\\ &10\left( \frac{29}{64}-\frac{31}{80} \right)= 10 \left( \frac{5·29-4·31}{320}\right)=\\ &\\ &\\ &10\left( \frac{145-124}{320} \right)= 10 \left(\frac{21}{320}\right)= \frac{21}{32}\end{align}$$Es un auténtico milagro que haya podido sobrevivir a esto, no sabes como cuesta hacer todo esto con el editor de ecuaciones.
Creo que ya me he merecido los puntos con esta parte y las otras dos no van a ir a la zaga en cuanto a dificultad. ¿Por qué no mandas las partes b y c cada una en una pregunta distinta? Tienen mucha más envergadura que muchas preguntas simples que respondo aquí.


