Estadística matemática con aplicaciones 2

a)

La función de distribución en un punto x es la integral definida de la función de densidad entre -infinito y ese punto. En la práctica hay muchas funciones de densidad que valen 0 hasta cierto punto y la integral tiene es punto como límite inferior

F(y) = $(c(2-t))dt entre 0 e y =

c[2t-(t^2)/2] entre 0 e y =

c[2y-(y^2)/2]

Y las condiciones de una función de distribución es que valga 0 en el -infinito y 1 en el infinito. Pero donde la función de densidad sea cero la de distribución no puede aumentar. En nuestro caso, F debe ser 0 en (-oo, 0] y 1 en [2, +oo) luego calculamos c a partir de estos supuestos

F(0) = 0 eso lo cumple sea cual sea c

F(2) = 1 ==> c [2·2-(2^2)/2] = 1 ==> c(4-2) = 1 ==> c = 1/2

b)

F(y) = 0 si -oo < y < 0

y - (y^2)/4 si 0 <= y <= 2

1 si 2 < y < +oo

c) Aquí están:

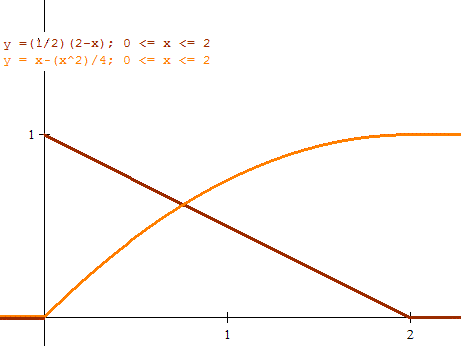
No estuve muy acertado eligiendo los colores. Vamos, qu no cambié los que me dio el programa. La de marrón más oscuro es la de densidad y la de marrón más claro la de distribución.

d) P(1 <= y <= 2) = F(2) - F(1) = 1 - [1 -(1^2)/4] = 1-(1-1/4) = 1-3/4 = 1/4

e) Dividimos el triangulo formado por función de densidad (marrón oscuro) y los ejes

En cuatro iguales al que se forma desde el punto 1 al 2. Luego el triangulo entre 1 y 2 tiene por área 1/4. Esa área es precisamente la probabilidad de que la función valga entre 1 y 2.

Y eso es todo.